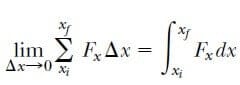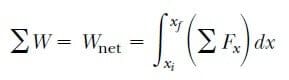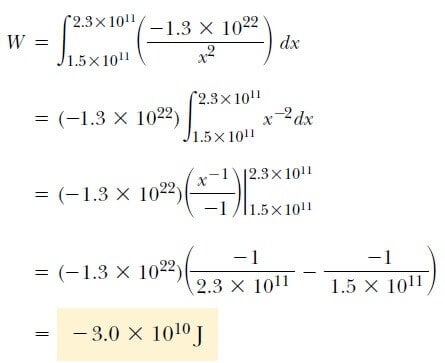Değişken Bir Kuvvetin Yaptığı iş

Merhaba arkadaşlar bu yazımızda sizlere değişken bir kuvvetin yaptığı iş ile ilgili konu anlatımı yapacağız. Bunun yanı sıra konuyu daha iyi anlamak içinde örnek çözeceğiz. Değişken bir kuvvetin etkisi altında ve x-ekseni boyunca yer değiştiren bir cismi inceleyelim. Bu cisim, x ekseni üzerinde x = x_i den x= x_f ye yer değiştirsin. Böyle bir durumda kuvvetin yaptığı işi hesaplamak için W = (FcosΘ)d yi kullanamayız. Çünkü bu bağıntı, sadece F büyüklük ve yönce sabit olduğunda uygulanır. Fakat, cismin Şekil 1a da tanımlanan küçük bir Ax yer değiştirmesi yaptığını düşünürsek, kuvvetin x bileşeni (F_x)bu aralıkta yaklaşık olarak sabit olur.

Bu durumda, bu küçük yer değiştirme için kuvvetin yaptığı iş

W = F_xΔx

olarak ifade edilebilir. Bu tam olarak Şekil 1a daki gölgeli dikdörtgenin ala­nıdır. F_x in x ile değişen eğrisini Şekil 1a daki gibi çok sayıda bu tip aralıklara böldüğümüzü düşünürsek, x_i den x_f ye olan yer değiştirme için yapılan toplam iş, yaklaşık olarak çok sayıdaki bu terimlerin toplamına eşit olur:

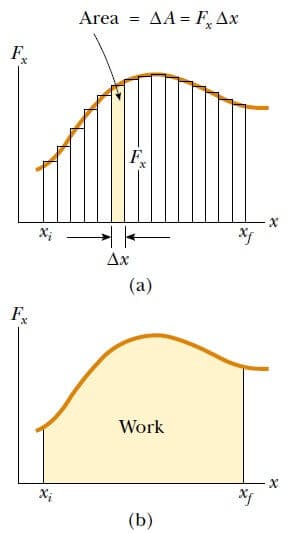
Şekil 1(a) Küçük Δx yerel eğiş t irme si için F kuvvetinin yaptığı iş Fx Δx dir. Bıı değer boyanmış dikdörtgenin alanına eşittir. x_i den x_f‘ye olan bir yer değiştirme için yapılan toplam iş, yaklaşık olarak tiım dikdörtgenlerin alanlarının toplamına eşittir, (b) Parçacık x_i’den x_f ye giderken F_x değişken kuvvetinin yaptığı iş tam olarak bu eğrinin altındaki alana eşittir.

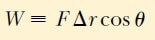
Yer değiştirmeler sıfıra yaklaştırılırsa, toplamdaki terimlerin sayısı sonsuza gider. Fakat toplamın değeri, F_x eğrisi ile x ekseninin sınırladığı gerçek alana eşit sonlu bir değere yaklaşır:

Bu belirli integral, sayısal olarak x_i ile x_f arasındaki F_x in x e göre değişim eğrisinin altındaki alana eşittir. Dolayısıyla, cismin x_i den x_f ye yer değiştirmesi halinde F_x in yaptığı iş

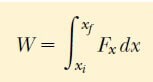
larak ifade edilebilir. F_x = FcosΘ sabit olduğunda bu eşitlik, 1 Eşitliğine indirgenir.

Bir parçacık üzerine birden fazla kuvvet eskirse, yapılan toplam iş, tam olarak bileşke kuvvetin yaptığı iştir. x doğrultusundaki bileşke kuvveti ∑F_x olarak ifade edersek, cismin, x_i den x_f ye hareket etmesi halinde yapılan net iş

Değişken Bir Kuvvetin Yaptığı iş ile ilgili Örnek

Değişken bir kuvvetin yaptığı iş ile ilgili örnek; Bir Uydu üzerinde Güneş’in yaptığı iş

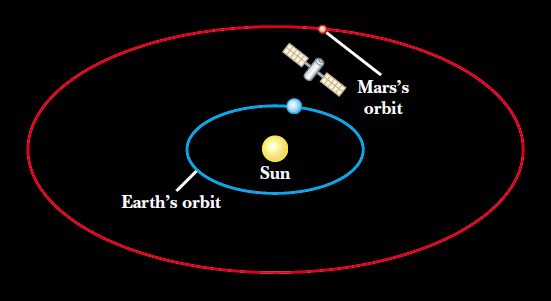
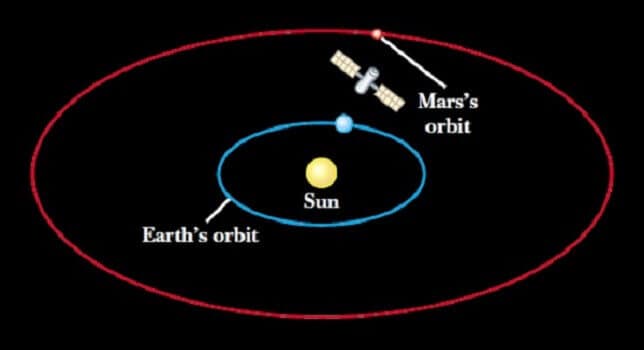
Şekil 2 de gösterilen gezegenler arası bir araştırma uydusu güneşe doğru

F=- 1,3 x 10 ²²/x²

büyüklüğünde bir kuvvetle çekilmektedir. Burada x, güneşten uyduya doğru ölçülen uzaklıktır. Uydu-güneş arasındaki uzaklık 1,5 x 10¹¹ m’den 2,3 x 10¹¹ m’ye değişirse güneşin uydu üzerinde yaptığı işi hesaplayınız.

Grafiksel Çözüm;

Kuvvet formülündeki eksi işareti, uydunun güneşe doğru çekildiğini gösterir. Uydu güneş­ten uzaklaştığı için, uydu üzerine yapılan iş için negatif bir değer hesaplamayı bekleriz.

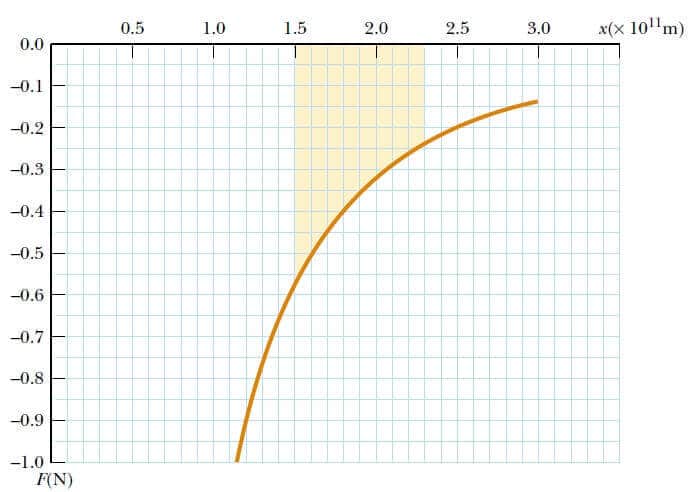
Bir hazır bilgisayar programı veya başka sayısal yollarla Şekil 3’dekine benzer bir grafik oluşturabilirsiniz. Grafikteki her bir küçük kare (0,05 N) (0,1 x 10¹¹ m) = 5 x 10⁸ N.m alanına karşılık gelir. Yapılan iş, Şekil 3’deki gölgeli alana eşittir. Yaklaşık 60 gölgeli alan olduğu için toplam alan ( x-ekseninin altında olduğu için negatiftir) – 3 x 10¹⁰ N m. dir. Bu, güneş tarafından uydu üzerinde yapılan iştir.

Analitik Çözüm; Güneşin uydu üzerinde yaptığı işi daha kesin hesaplamak için 2 Eşitliğini kullanabiliriz. Bu integrali çözmek için;

Bu yazımızda sizlere değişken bir kuvvetin yaptığı iş ile ilgili konu anlatımı yaptık. Diğer yazılarımızda görüşmek üzere.