Merhaba arkadaşlar bu yazımızda sizlere genel görelilik kuramı ve genel görelilik kuramı formüllerini, bunun yanı sıra genel görelilik kuramını daha iyi kavramanız için sizlere yazımızın en sonunda özet anlattım. Kütle görünüşte farklı iki göreve sahiptir: diğer kütlelerle etkileşmek için kütle-çekimi ve ivmelenmeye karşı koymak için eylemsizlik görevi. Bu iki özelliği temsil etmek için g ve i alt indislerini kullanarak yazalım.
- Kütle-çekimi özelliği Fg=mgg
- Eylemsizlik özelliği ∑F = mia
Evrensel kütle-çekimi sabiti G’nin değeri mg ve mi nin büyüklüklerini sayısal olarak eşit yapacak şekilde seçilmiştir. Ancak G’nin nasıl seçildiğine bağlı olmaksızın mg ve mi arasındaki orantılık deneysel olarak 1012 de birkaç gibi çok yüksek duyarlılıkla tespit edilmiştir. Sonuç olarak kütle-çekimi kütlesi ile eylemsizlik kütlesinin gerçekten tam tanıma orantılı oldukları görülmektedir.
Fakat neden bu böyledir? Bu kütle tanımları birbirleri ile bütünüyle farklı iki kavrama dayalıdırlar: iki kütle arasındaki karşılıklı kütle-çekimi kuvveti ve tek bir parçacığın hızlandırılmasına karşı direnişi. Newton ve diğer pek çok fizikçiyi yıllarca oyalayan bu soru, Einstein 1916 da genel görelilik teorisi olarak bilinen kütle-çekimi kuramını yayınlandığında cevaplanabildi. Einstein’in bu çalışması matemaktiksel olarak karmaşık bir teori olduğundan, biz burada yalnızca kuramın şıklığı ve derinliği hakkında basit ipuçları vereceğiz.
Einstein’in görüşüne göre, mg ve mi nin birbirleri ile orantılı olarak görünmeleri, olağanüstü rastlantısı, bu iki kavram arasındaki kaçınılmaz ve temel bir bağlantının varlığının delilidir. Einstein hiç bir mekanik deneyi (bir kütlenin serbest düşüşü gibi) Şekil 39.22 a ve b de gösterilen iki durumu birbirinden ayırt edemeyeceğine işaret etti. Her iki halde de çanta aşağıya doğru g ivmesine sahip olacaktır.
Albert Einstein bu fikri daha da genişleterek mekanik veya başka bir tür hiçbir deneyin bu iki durumu birbirinden ayırt edemeyeceğini öne sürdü. Bu tartışmanın mekanik kökenlileri yanı sıra, diğer tüm olayları içine alacak şekilde genişletilmesi ilgi çekici sonuçlan ortaya çıkarır. Örneğin; Şekil 39.22c’de görüldüğü gibi bir ışık atmasının yatay olarak asansör boyunca yollandığını düşünelim. Işığın asansörün sağ duvarına varması için geçen süre içinde duvar yukarıya doğru hızlanacaktır. Bu ışığın asansör hareketsiz olsaydı duvarda varacağı noktadan daha aşağıdaki bir noktada duvara varmasına neden olur. Böylece asansör referans sisteminde ışık atmasının yörüngesi, asansör yukarı doğru ivmelendiği için aşağıya doğru bükülür. İvmeli hareket yapan asansör, m içindeki ivmesiz asansörden ayırt edilemeyeceğinden, Einstein kütle-çekimi alanı tarafından da aşağıya doğru bükülmesi gerektiğini öne sürdü. Küçük olmasına rağmen deneyler bu etkiyi doğrulamıştır. Ufka doğru yollanan bir lazer ışını 6000 km yol aldığında yeryüzüne doğru 1 cm bükülmüştür.(Newton’ nun kütle çekim teorinde böyle bir bükülme öngörülemez.)
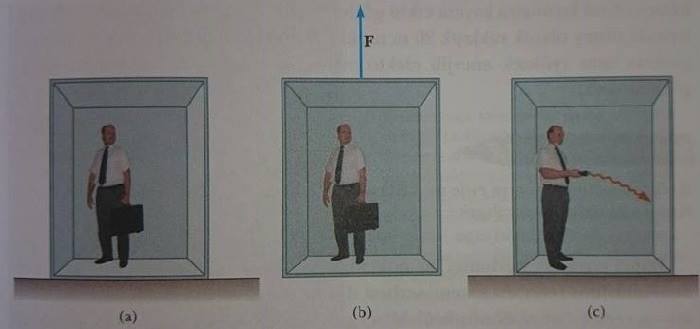
Şekil 39.22 (a) Gözlemci homojen kütle-çekimi alanı g içinde hareketsizdir, (b) Gözlemci kütle çekiminin ihmal edilebileceği bir yerdedir, ancak referans sistemi g ivmesi yaratan bir dış, F kuvveti tarafından çekilmektedir. Einstein’a göre (a) ve (b) deki referans sistemleri bütünüyle eşdeğerdirler. Hiçbir yerel deneyle iki sistem arasındaki fark algılanamaz, (c) (a) ve (b) deki sistemler gerçekten eşdeğer iseler, Einstein’in öngördüğü gibi ışık ışını kütle çekimi alan, içinde eğilmelidir.
Einstein genel görelilik kuramının iki pastülatı şunlardır:
- Bütün doğa yasaları, ivmeli hareket yapan veya yapmayan bütün referans sistemlerindeki gözlemciler için aynı biçime sahip olmalıdırlar.
- Herhangi bir nokta civarında kütle-çekimi alanı, kütle-çekimi etkileri yok iken ivmelendirilen bir referans sistemine eşdeğerdir. (Bu eşdeğerlik ilkesidir.)
İkinci pastülat kütle-çekimi kütlesi ile eylemsizlik kütlesinin yalnızca orantılı değil ama bütünüyle eşdeğer olduğunu ima eder. İki farklı kütle türü olarak düşüne geldiklerimiz gerçekte özdeştirler.
Genel görelilik teorisinin ilgi çekici öngörülerinden biri, zaman ölçümünün kütle-çekimi tarafından değiştirilmesidir. Kütle-çekimi alanı etkisi altındaki bir saat, kütle-çekiminin ihmal edilebileceği bir yerde bulunan saate göre daha yavaş işler. Sonuç olarak şiddetli kütle-çekimi alanı etkisi altındaki atomlardan yayınlanan radyasyonun frekansı, zayıf kütle-çekimi alanı içinde yayınlanan aynı radyasyonla kıyaslandığında daha düşük frekanslara, kırmızıya kayar. Büyük kütleli yıldızlar tarafından yayınlanan ışığın spektrum çizgilerinde bu kütle-çekimi kırmızıya kayma etkisi gözlenmiştir. Aynı etki, dünya üzerinde aralarında düşey olarak yaklaşık 20 m uzaklık bulunan çekirdeklerden yayınlanan gamma ışını (yüksek enerjili elektromanyetik radyasyon) frekanslarında da gözlenmiştir.
İkinci pastülat, herhangi bir noktadaki kütle-çekimi alanının, uygun bir ivmelendirilmiş referans sistemi serbest düşme hareketi yapan bir referans sistemi seçersek “sıfıra dönüştürülebileceğini” söyler. Einstein kütle-çekimi alanını “yok etmek” için ivmenin gerekli olduğunu anlatmak için ustaca bir yöntem geliştirmiştir. Her noktada kütle-çekimi etkisini açıklayan uzay—zaman eğriliği kavramını belirlemiştir. Gerçekte uzay-zaman eğriliği bütünüyle Newton’un kütle-çekimi teorisinin yerini alır. Einstein’a göre kütle-çekimi kuvveti diye bir şey yoktur. Daha doğrusu kütlenin varlığı çevresinde uzay-zaman eğriliğine neden olur ve bu eğrilik serbestçe hareket eden cisimlerin izlemesi gereken uzay zaman yörüngesini belirler. 1979 da John wheeler, Einstein’in genel görelilik teorisini tek bir cümle ile özetlemişti: “Uzay maddeye nasıl hareket edeceğini söyler, madde de uzaya nasıl eğrileceğini söyler.”
Dünya üzerinde farklı iki noktadan yola çıkarak Kuzey Kutbuna doğru yürüyen iki yolucuyu düşünelim. Her iki yolcu da kuzeye doğru gittiklerini söylemelerine ve yollarının birbirine paralel olması gerektiğine rağmen, sanki onları birbirine çeken bir kuvvet varmış gibi yürüdükçe birbirlerine yaklaşırlar. Dünya yüzeyinin eğriliği bu etkiyi ortaya çıkarır. Benzer yolda iki kütle arasındaki kütle-çekimi kuvveti olarak düşünmeye alıştığımız olgu, Einstein’in görüşüne göre kütlelerin uzay-zaman bükülmesi ve sonuç olarak yatak örtüsü üzerinde iki ağır bilyenin bir araya gelmesine benzer şekilde birbirlerine doğru hareket etmeleridir.
Genel görelilik kuramının öngörülerinden biri, Güneşin yakınından geçen bir ışık ışınının Güneşin kütlesi nedeniyle yaratılan eğri uzay-zaman içinde sapmasının gerektiğidir. Bu öngörü 1. Dünya Savaşından hemen sonra ortaya çıkan tam güneş tutulması sırasında Güneşin yakınından geçen yıldız ışıklarının sapması astronomlar tarafından gözlendiğinde doğrulanmıştır (Şek. 39.23). Bu keşif dünyaya duyurulduğunda, Einstein uluslararası bir üne kavuşmuştur.
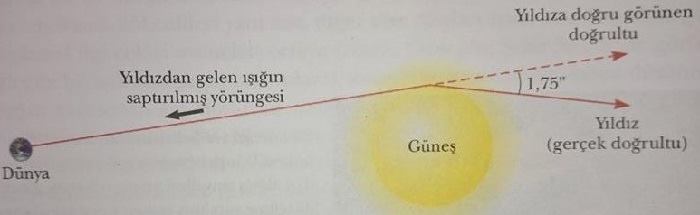
Şekil 39.23 Güneşin yakınından geçen yıldız ışığının sapması. Bu etki nedeniyle Güneş veya bazı diğer uzak gök cisimleri kütle-çekimi merceği gibi iş görebilirler. Einstein genel görelilik teorisi çalışmasında Güneş yüzeyini yalayarak geçen yıldız ışığının 1,75″ kadar sapması gerektiğini hesaplamıştı.
Büyük bir yıldızın nükleer yakıtını bitirip, çok küçük bir hacme çökmesi ile oluşabileceğine inanılan çok büyük kütle yoğunluğu ortaya çıkarsa bir kara delik oluşabilir. Bu halde uzay zaman eğriliği o kadar büyüktür ki, kara deliğin merkezinden belli bir uzaklık içinde tüm madde ve ışık kara delik tarafından yutulur.
Genel Görelilik Kuramı Özet
Özel görelilik kuramının iki temel pastülatı şunlardır:
- Fizik yasaları bütün eylemsiz referans sistemlerinde aynı olmalıdırlar.
- Boşlukta ışık hızı bütün eylemsiz referans sistemlerinde, gözlemcinin hızı veya ışık kaynağının hızı ne olursa olsun c=3,00 x 108 ııı/s değerine sahiptir.
Özel görelilik teorisinin üç sonucu şunlardır:
- Bir gözlemciye göre eşzamanlı olan olaylar, birinciye göre hareketli olan diğer bir gözlemciye göre eşzamanlı değildirler.
- Bir gözlemciye göre hareketli saatler γ= (1 — v2/c2)-1/2 çarpanı kadar yavaşlamış gibi görünürler. Bu olay zaman genişlemesi olarak bilinir.
- Hareketli cisimlerin uzunluğu hareket doğrultusunda l/γ = (1 – v2/c2)1/2 çarpanı kadar büzülmüş gibi görünür. Bu olay uzunluk büzülmesi olarak bilinir.
Özel görelilik pastülatlarının sağlanabilmesi için Galileo dönüşüm bağlantıları yerine Lorentz dönüşüm eşitlikleri alınmalıdır.
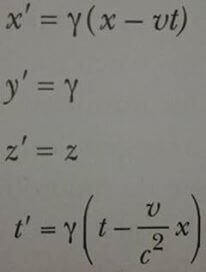
buradan
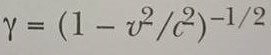 dır.Hız dönüşüm eşitliğinin göreli (rölativistik/izafi) şekli
dır.Hız dönüşüm eşitliğinin göreli (rölativistik/izafi) şekli
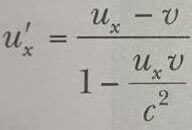
gibidir, burada ux cismin S sistemindeki, u’x ise S’ sistemindeki hızıdır.
u hızıyla hareket eden bir parçacığın doğrusal (çizgisel/lineer) momentumunun göreli ifadesi şöyledir.
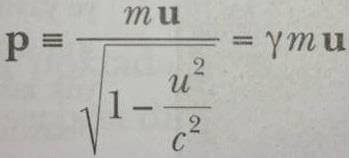
Bir parçacığın kinetik enerjisi için göreli ifade
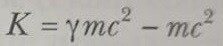
gibidir, burada mc2 ye parçacığın durgun enerjisi adı verilir.
Bir parçacığın toplam enerjisi E, kütlesi m ye meşhur kütle-enerji eşdeğerliliği ifadesi ile bağlıdır:
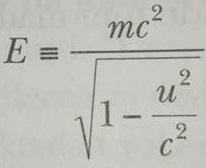
Göreli doğrusal momentum toplam enerjiye aşağıdaki eşitlik ile bağlıdır:
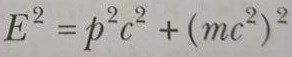
Genel görelilik kuramı başlıklı yazımı burada sizlerle paylaştım. Diğer yazımda görüşmek üzere. Kaynak: Serway Kitabı