Graf teorisi ve elini kaldırmadan çizmeyi birçoğumuz ilkokul yıllarımızda karşılaşmışızdır. Ya arkadaşlarımız bizlere yada bizler onlara resimdeki şekli hiç el kaldırmadan çizip çizemeyeceğini sormuşuzdur ve hepimiz birkaç denemeden sonra sonucuna ulaşmışızdır. Ancak hiçbirimiz bunun aslında çok basit bir Matematik problemi olduğu bilmiyorduk.
Problemin aslı 1700′ lü yılların meşhur problemi olan “Königsberg’in 7 köprüsü” problemidir. Königsberg şehri Pregel nehrinin kıyısına kurulmuş ve 7 ayrı köprü ile birbirine bağlanmış 4 farklı bölümden oluşmaktadır (Resimde görüldüğü üzere).
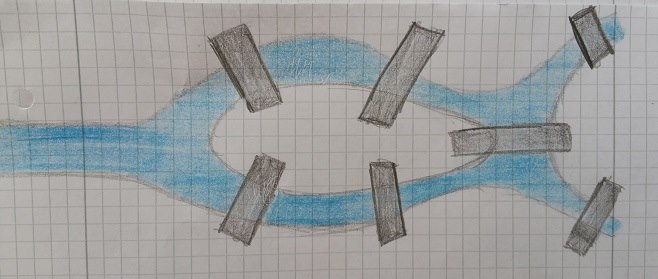
Zamanla insanlar kendilerine, aynı köprüden bir kez daha geçmemek üzere tüm şehri dolaşmanın mümkün olup olmadığı sorusunu sormuşlardır. Ancak hiç kimse böyle bir rota çizemedi, dönemin meşhur matematikçilerinden biri olan Leonhard Euler’ de dahil, fakat Euler bunun neden mümkün olamayacağını ispatlayabilmiştir.
Euler problemin ispatı için şekli daha basit bir hale getirmiştir, bunun için köprüleri çizgiler ve şehir parçalarınıda noktalar halinde ifade etmiştir. Bunun sonucu olarak aşağıdaki şekil ortaya çıkmıştır.
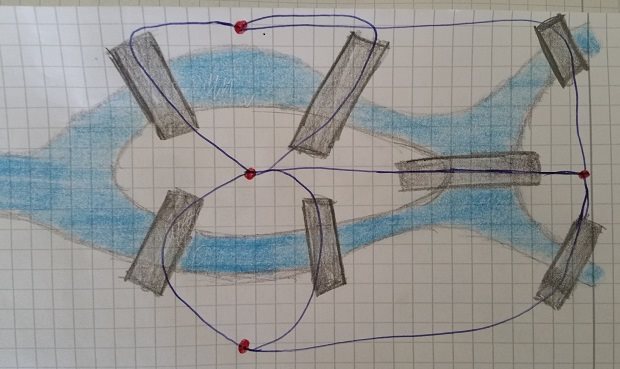
Resimden sadece çizgi ve noktaları alacak olursak:
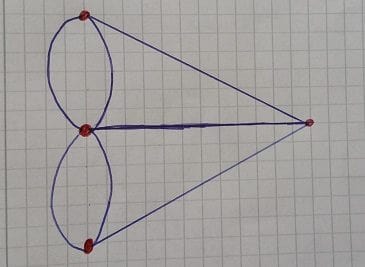Euler böyle bir gezinin mümkün olabilmesi için her noktada buluşan çizgilerin toplam sayısının çift rakam olması gerektiği kanısına varmıştır. Bu sayede bir noktaya ulaşmak için köprülerden birisi, çıkmak içinse diğeri kullanılacaktı. Ancak ortada bir istisna vardı, başlangıç ve bitiş noktaları. Başlangıç ve bitiş noktalarının farklı olduğu durumlarda bu iki noktanın sadece tek bir çizgi ile diğer noktalara bağlı olması gerekiyordu. Başlangıç ve bitiş noktalarının aynı olduğu durumlarda ise her noktanın çift sayıda köprüye ihtiyacı vardır. Bütün bu düşünceler ışığında Euler genel bir teoremi ortaya çıkartmıştır. Bu teoreme göre böyle bir gezintiyi mümkün kılabilmek için sistemdeki her bir noktaya ulaşan toplam çizgi saysının çift olması yada en fazla iki noktaya ulaşan toplam çizgi sayısının tek olması zorunluydu.
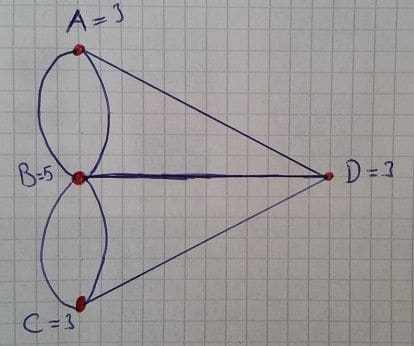Bu teoremi Königsberg problemine uygulayan Euler A noktasına toplam 3, B noktasına 5, C noktasına 3 ve D noktasına toplamda 3 köprü ulaştığını görmüş ve teoremine göre böyle bir gezinin imkansız olduğunu kanıtlamıştır.
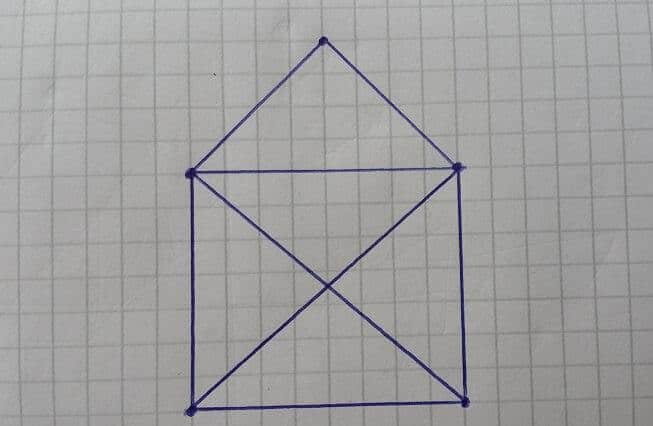
Bizler de Euler teoremini ilkokul yıllarımızın bulmacasına uyguladığımız zaman şeklin gerçekten de hiç el kaldırılmadan çizilebildiğini ispatlayabiliriz.
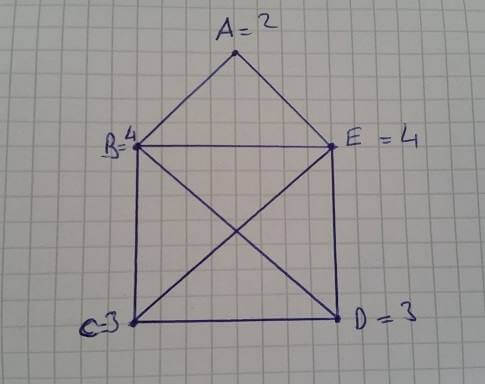
Resimde görüldüğü üzere A noktasına toplam 2, B noktasına 4, C noktasına 3, D noktasına 3 ve E noktasına 4 çizgi ulaşmaktadır. Euler teoremine göre sistemde en fazla 2 noktaya ulaşan çizgi sayısının tek, geri kalanların çift yada tüm noktalara ulaşan çizgi sayısının çift olması gerekmekteydi. Bizim sistemimiz bu teoreme uygun olduğu için, şeklin hiç el kaldırılmadan çizilebileceğini ispatlamış olduk.
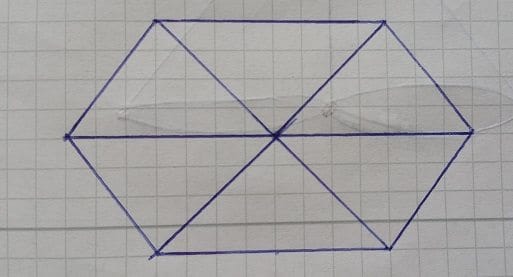
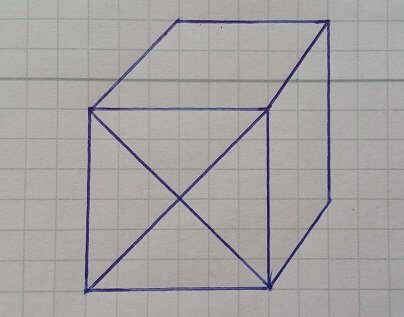
Sizlerde bu teoremi kullanarak aşağıdaki şekillerin hiç el kaldırmadan çizilip çizilemeyeceğinin ispatını yapabilirsiniz.
