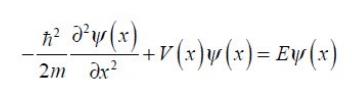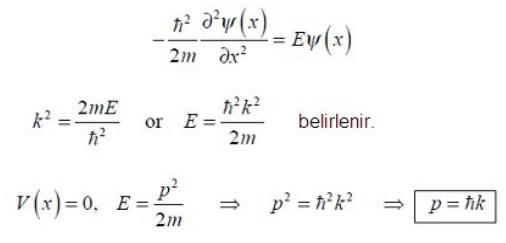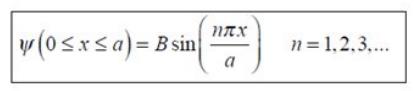Kuantum Teorisi şüphesiz 20. yüzyıl bilim camiasını en derinden etkileyen ve klasik fizikte yeni çığırlar açan dev bir akım olmuştur. Bu dev akım pek çok yönden eleştirilmiş, üzerine kafa yorulmuş ve fizik camiasının ufkunu genişletmiştir. Bu yazımız schrödinger denklemi nedir, schrödinger denklemi çözümü ve schrödinger denklemi çıkarılışı hakkında olacak.
Schrödinger Denklemi
Kuantum mekanikleri tek bir yazıda anlatılamayacak kadar detaylı ve derin olsa da yıllardır dillerden düşmeyen Schrödinger denklemini şu şekilde özetleyebiliriz. Erwin Schrödinger dalga mekaniği üzerine çalışırken ortaya çıkan kuantum furyasıyla birlikte Schrödinger denklemini ileri sürmüştür. Denklem kuantum problemleri üzerinde oldukça başarılı olmuştur ve esas olarak Werner Heisenberg’in belirsizliği ile Louis de Broglie’nin dalga-parçacık birlikteliğini almıştır. Denklemin ortaya çıkışı dalga fonksiyonları ile başlamıştır. Dalga fonksiyonları, bir parçacığın de Broglie’nin öne sürdüğü şekilde eşlikçi dalgasının matematiksel ifadeleridir.
Adım Adım Schrödinger Denklemi Çözümü:
Şekildeki ifade düzenli sinüs dalgaları oluşturan harmonik bir osilatörün genel dalga denklemidir. İfadeyi diferansiyel bir formda yazacak olursak;
İfadenin yeni halini çıkarırsak dalga fonksiyonunun x koordinatına göre 1. türevi olduğunu görürüz. İfadenin 2. türevini alıp, ifadede dalga fonksiyonunu tekrar yerine yazarsak ifadenin yeni şekli;
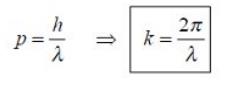
İfadedeki k, dalga katsayısı ya da numarası olarak adlandırılır ve dalga vektörünün büyüklüğüdür. Dalga boyu(λ) ile k arasındaki bağıntı;
Bununla birlikte dalga boyunu de Broglie’nin denkleminden de elde edebiliriz. k’yi de Broglie denkleminden elde edecek olursak; Klasik mekanikte bir objenin toplam mekanik enerjisini kinetik enerjisi ile potansiyel enerjisinin toplamı şeklinde yazabiliriz. Eşitlikten kinetik enerjiyi çekersek; Kinetik enerji ifadesini kütle ile çarptığımızda karşımıza çıkan mv çarpımının yani çizgisel momentumun karesini elde ederiz ve bu ifadeyi tekrar de Broglie ifadesinde denkleme yazarsak ortaya çıkan yeni ifade;
Denklem bu haliyle büyük ölçüde tamamlanmış bir haldedir. Bu haliyle denklem sadece x koordinatına bağlı olarak tek boyutlu bir kartezyen koordinatta çözüm verecektir. Denklemi 3 boyutlu kartezyen koordinatlarda yazarsak; Denklemin sol tarafındaki dalga fonksiyonunun x, y ve z kartezyen koordinatlarına göre 2. dereceden parçalı türevlerinin toplamı kısaca Laplasyen operatörü ile ifade edilir. Bununla birlikte denklemdeki Planck sabitini(h) indüklenmiş Planck sabiti(ℏ=h/2π) olarak çekersek; Klasik mekanikte kinetik enerjinin çizgisel momentum(p) cinsinden yazılışı;
Bu noktada dikkat edileceği üzere çizgisel momentum ifadesine karşılık gelen operatörü denklemden çıkarabiliriz. Bu durumda; Sıra elimizdeki denklemi son haliyle yazmaya geldiğinde Schrödinger Denklemi;
Denklemin sol tarafındaki H; Hamiltonyen operatörüdür, parçacığın sahip olduğu toplam enerjiyi ifade eder ve dalga fonksiyonunun sağ taraftaki eigenvalue enerji operatörüne dönüşümünü sağlar.
Schrödinger denklemi pek çok konfigürasyon için doğru sonuçlar verse de halen kuantum mekaniğini mütemadiyen açıklamada yeterli olamamaktadır, eksikleri vardır. Ancak bununla birlikte fizik camiasında büyük atılımlara temel oluşturmuştur. Kuantum alan kuramından rölativistik kuantum mekaniğine kadar pek çok konuda çıkış noktası olmuştur.