Newton, evrensel kütle çekim teorisini yayınladığında, gezegenlerin hareketini doyurucu bir tarzda açıkladığından bu teori bir başarı olarak kabul edilmişti. 1687 den beri bu teori, kuyruklu yıldızların hareketleri, Cavendish terazisinin sapması, çift yıldızların yörüngeleri ve galaksilerin dönmesini açıklamakta kullanılmıştır. Bununla beraber, gerek Newton’un çağdaşları ve gerekse ondan sonra gelenler, uzaktan etki eden bir kuvvet kavramını kabul etmekte zorlandılar. Birbiriyle temas halinde olmadan, iki cismin nasıl olup ta birbiri ile etkileştiğini soruyorlardı. Bu soruyu Newton kendisi açıklayamamıştı.
Temasta olmayan cisimler arasındaki etkileşmeyi açıklayan bir yaklaşım Newton’un ölümünden bir hayli zaman sonra geldi ve kütle çekimi etkileşmesine farklı bir tarzda bakmamızı sağladı. Anlatıldığı gibi, bu alternatif yaklaşım uzayda her noktada var olan bir kütle çekim alanı fikrini kullanır. Kütlesi m olan bir parçacığa, alanın g olduğu bir noktaya konulduğu zaman F = mg kuvveti etkir. Başka deyişle, alan parçacık üzerine bir kuvvet uygular.
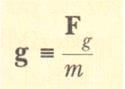
Buradan, çekim alanı g, olarak tanımlanır. Yani, uzayda herhangi bir noktadaki çekim alanı, o noktadaki bir deneme kütlesinin maruz kaldığı kuvvetin, o deneme kütlesiyle bölümüne eşittir. Alanın var olması için deneme parçacığının bulunmasının gerekli olmadığına dikkat ediniz. Çekim alanını Dünya oluşturmaktadır. Alanı oluşturan cisme kaynak parçacık deriz. (Her ne kadar dünya açıkça bir parçacık değilse de böyle bir ifadeyi kullanabiliriz; biraz sonra, oluşturduğu kütle çekim alanını anlatırken Dünya’yı bir noktasal parçacık olarak alabileceğimizi tartışacağız). Alanın içine bir deneme parçacığı yerleştirerek ve onun üzerine etki eden kuvveti dikkate alarak alanın varlığım algılayabilir ve şiddetini ölçebiliriz.
Her ne kadar kütle çekim kuvveti anlam olarak iki cisim arasındaki bir etkileşme ise de, kütle çekim alanı kavramı bize, cisimlerden birinin kütlesini ön “çarpan” olarak alma imkanını verir. Esas olarak, bir cismin (şimdiki halde, Dünya) etrafındaki boş uzay üzerine yaptığı etkiyi, ikinci bir cismin bu uzayda herhangi bir yerde bulunması halinde var olacak kuvvet cinsinden tasvir ediyoruz.
Alan kavramının nasıl işlendiğine bir örnek olarak Dünya yüzeyinin yakınında bulunan m kütleli bir cismi düşününüz. Cisme etkiyen çekim kuvveti GM m/r büyüklüğüne sahip olduğundan Dünya’nın merkezinden r uzaklığındaki bir noktada g alanı
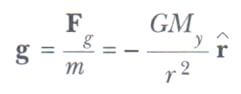
ile verilir. Burada r radyal (ışınsal) olarak Dünya’dan dışarıya doğu yönelmiş bir birim vektördür ve eksi işareti alanın, Şekil’de da gösterildiği gibi, Dünya’nın merkezine doğru yöneldiğini gösterir. Dünya’yı çevreleyen değişik noktalardaki alan vektörlerinin hem doğrultusu ve hem de büyüklük bakımından değiştiğine dikkat ediniz. Dünya yüzeyi yakınındaki küçük bir bölgede, aşağı doğru olan g alanı Şekil’de gösterildiği gibi yaklaşık olarak sabit ve düzgündür. Dünya’nın küresel olduğu kabul edilirse, Dünya’nın dışındaki bütün noktalarda geçerlidir. Dünya yüzeyinde r = Ry’dir ve g’nin sahip olduğu büyüklük 9,80N/kg dır.
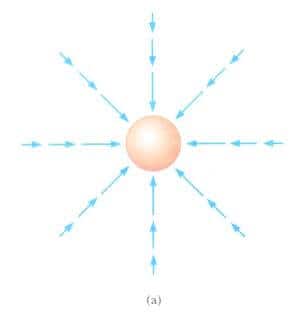
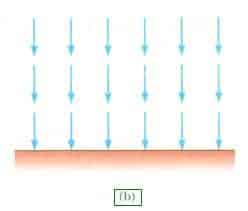
(a) Dünya gibi, düzgün küresel bir cisim yakınındaki kütle çekim alanı vektörleri hem doğrultu hem de büyüklük bakımından değişirler. Vektörler, alan içine konulan bir parçacığın sahip olacağı ivme yönündedir. Herhangi bir yerdeki alanın büyüklüğü, bu konudaki serbest düşme ivmesinin büyüklüğü kadardır, (b) Dünya yüzeyi yakınındaki küçük bir bölgede kütle çekim alanı vektörleri, gerek yön gerekse büyüklük bakımından düzgündür.

