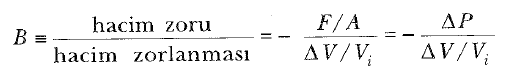Bu yazımızda sizlere katıların esneklik özellikleri, young modülü (uzunlukta esneklik), kesme modülü (şeklin esnekliği) ve bulk modülü(hacim esnekliği) konularını anlatacağız. Mekanik konusunu işlerken, şu ana kadar, cisimlerin üzerine dış kuvvetler etki ettiğinde, onların bozulmadığını kabul ettik. Gerçekte, bütün cisimler bozulabilirler. Yani, dış kuvvetlerin uygulanması halinde, bir cismin şeklinin veya büyüklüğünün (veya bunların her ikisinin) değişmesi mümkündür. Gerçi bu değişimler olurken, cismin içindeki iç kuvvetler, bozulmaya karşı direnç gösterirler.
Katıların bozulmasını zor ve zorlanma kavramlarından yararlanarak açıklayacağız. Zor, bozulmaya sebep olan kuvvetle orantılı bir niceliktir. Daha açık olarak, zor, cismin üzerine birim kesit başına etki eden dış kuvvetir. Zorlanma ise bozulmanın derecesinin bir ölçüsüdür. Yeteri kadar küçük zorlar için; zorlanmanın, zorla doğru orantılı olduğu ve orantı sabitinin bozulan maddenin cinsine ve bozulmanın yapısına bağlı olduğu görülür. Bu orantı sabitini esneklik sabiti (veya esneklik modülü) olarak adlandıracağız. Böylece, esneklik sabiti, zorun zorlanmaya oranı olarak,
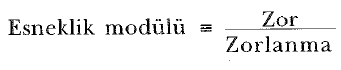
Katıların Esneklik Özellikleri Nelerdir
Katıların esneklik özellikleri için bozulmanın üç değişik şeklini göz önüne alacağız ve bunların her biri için bir esneklik modülünü tanımlayacağız:
1. Katının, uzunluğundaki bir değişime karşı gösterdiği direncin bir ölçüsü olana “Young sabiti” (Young modülü).
2. Katının, atomik düzlemlerinin birbiri üzerinde kayması şeklinde ortaya çıkan harekete karşı gösterdiği direncin bir ölçüsü olan ‘ kesme sabiti” (makaslama modülü).
3. Katıların veya sıvıların, hacimlerinde meydan gelecek değişime karşı gösterdikleri direncin bir ölçüsü olan hacim (bulk ) modülü.
Young Modülü: Uzunlukta Esneklik
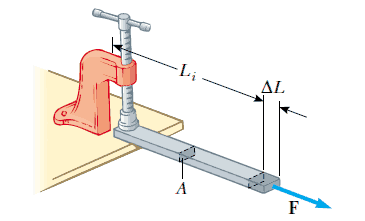
Kesitinin alanı A olan Li uzunluğundaki bir çubuğun, Şekil 1 ’de gösterildiği gibi, bir ucundan mengeneyle tutturulduğunu düşünün. Çubuk boyunca, kesitine dik olacak şekilde, bir F dış kuvveti uygulandığında, çubuğun içindeki iç kuvvetler uzunluk değişimine karşı koymaya çalışır. Sonuçta, çubuk bir dengeye ulaşır. Denge durumunda, çubuğun uzunluğu L ’den daha büyük bir Lson uzunluğuna ulaşmış ve dış kuvvet, iç kuvvetler tarafından tam olarak dengelenmiştir. Böyle bir durum için, çubuğun zor etkisinde olduğu söylenir. Dış kuvvetin F büyüklüğünün çubuğun A kesit alanına oranı olarak, gerilme zorunu tanımlarız. Bu durumda gerilme zorlaması çubuğun uzunluğundaki ΔL değişiminin, çubuğun ilk uzunluğu olan Li ’a oranı olarak tanımlanır ve böylece boyutsuz bir nicelik elde edilmiş olur. Şimdi artık Young modülünü tanımlamak için (1) eşitliğini kullanabiliriz:

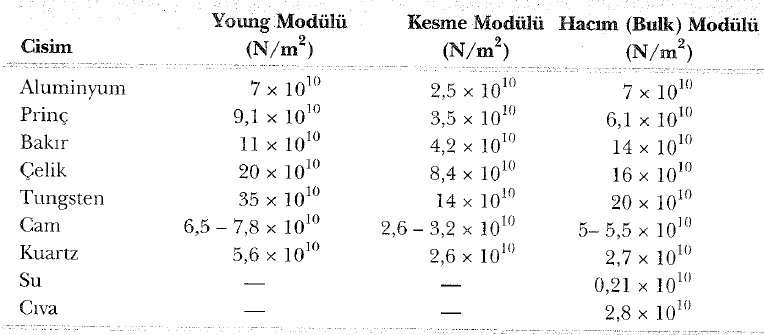
Bu nicelik, genellikle, gerilme veya sıkıştırılma sonucu zor etkisi altında bırakılan bir çubuk veya teli karakterize etmek için kullanılır. Zorlanma boyutsuz bir nicelik olduğundan, Y, birim alan başına kuvvet birimine sahiptir. Bazı maddelerin Young sabitleri, Tablo 1 ’de verilmiştir. Deneyler, (a) uygulanan sabit bir kuvvetin etkisi altında uzunlukla meydana gelen değişmenin, başlangıç uzunluğuyla orantılı okluğunu, (b) verilen bir zorlanmayı meydana getirmek için gerekli kuvvetin, kesit alanıyla orantılı olduğunu göstermektedir. Bu gözlemlerin her ikisi, (2) eşitliğiyle uyuşmaktadır.
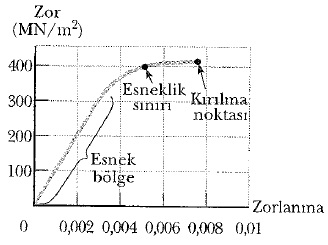
Bir cismin esneklik sının, o cisim kalıcı olarak bozulana kadar cisme uygulanabilen en büyük zor olarak tanımlanır. Yeteri kadar büyük bir zor ugulana-rak bir cismin esneklik sınırını geçmek mümkündür (bak şekil 2). Başlangıçta, zor-zorlanma eğrisi doğru bir çizgidir. Halbuki zor yeteri kadar artırılırsa eğri artık doğru şeklini yitirir. Zor esneklik sınırını geçtiğinde, cisim giderek aşırı derecede bozulur ve artık zor ortadan kalktıktan sonra bile başlangıçtaki şekline geri dönemez. Bunun sonucu olarak ta, cismin şekli kalıcı olarak değişir. Zor daha fazla artırıldığında, cisim eninde sonunda kopar.
Kesme Modülü: Şeklin Esnekliği
Cismin bir yüzü fs sürtünme kuvveti tarafından sabit bir konumda tutulurken, öteki yüzüne, yüzeye teğet bir F kuvveti uygulandığında, bozulmanın bir başka şekli ortaya çıkar (Şekil 3a). Cisim başlangıçta dikdörtgenler prizması şeklinde bir bloksa, kesme zoru, onun şeklini ara kesiti paralelkenar olan bir yapıya dönüştürür. Bu durumun doğmasına sebep olan zora kesme (makaslama) zoru denir. Bir kitabın Şekil 3b ’de gösterildiği gibi bir yüzüne bastırılarak itilmesi, kesme zoru altındaki cisimlere iyi bir örnektir. Küçük yer değiştirmeler için bu bozulma sonucunda cismin hacmi değişmez.
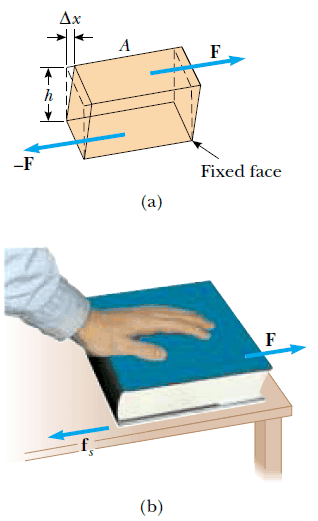
Kesme zorunun uygulandığı yüzeyin alanı A ise, kesme zoru, teğet F kuvvetinin yüzeyin alanına oranı olarak F/A şeklinde tanımlanır. Kesme zorlanması ise Δх/h oranı olarak tanımlanır. Burada Δx, kesilen yüzün uygulanan kuvvet doğrultusundaki yer değiştirmesi, h ise cismin yüksekliğidir. Bu büyüklükler cinsinden, kesme modülü,
olur. Bazı maddelerin kesme modülleri Tablo 1′ de verilmektedir. Kesme modülünün birimi, birim alan başına kuvvettir.
Bulk Modülü: Hacim Esnekliği
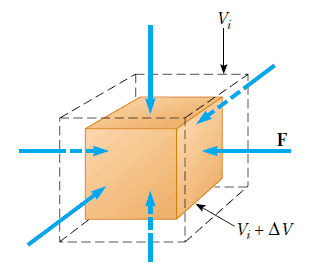
Son olarak, düzenli bir şekilde sıkıştırılan bir cismin buna karşı koyma özelliğini ifade etmek için hacim modülünü tanımlayalım. Bir cisme etki eden dış kuvvetlerin, cismin bütün yüzlerine dik açılarda etki ettiğini ve bütün yüzlere düzgün olarak dağıldığını kabul edelim (Şekil 4). 15. Kuvvetlerin bu şekilde düzgün olarak dağılması bir cismin bir akışkan içindeyken oluşur. Bu yapıdaki bir bozulmaya uğrayan cismin hacmi değişir fakat şekli aynı kalır. Hacim zoru, yüzeye dik olan F kuvvetinin büyüklüğünün, yüzeyin A alanına oranı olarak tanımlanır. P = F/A niceliğine basınç denir. Eğer bir cismin üzerindeki basınç ΔP= ΔF/A değeri kadar değişirse, o zaman cisim ΔV hacim değişimine uğrayacaktır. Hacim zorlanması, hacimdeki ΔV değişiminin başlangıçtaki V hacmine bölümüne eşittir. Böylece, (1) eşitliğinden, hacimdeki (bulk) küçülmeyi, bulk modülü olarak,
şeklinde tanımlarız. Bu tanım ifadesindeki eksi işareti В ‘nin artı işaretli bir sayı olmasını sağlamak için konulmuştur. Çünkü, basınçtaki bir artma (artı ΔP), hacmin küçülmesine (eksi ΔV ’ye) sebep olur. Basınç küçülürse (eksi ΔP), hacim büyür (artı ΔV).
Tablo 1 ’de bazı maddelerin hacim modülleri verilmektedir. Bu tablodaki değerlere başka bir kaynaktan bakarsanız, zaman zaman hacim (bulk) modüllerinin tersinin listelendiğini göreceksiniz. Bulk modülünün tersine, maddenin sıkışabilirliği denir.
Tablo 1 den, katıların ve sıvıların her ikisininde bulk modülüne sahip oldukları görülür. Bunun yanında, sıvılar için kesme modül ve Young modülü yoktur. Çünkü bir sıvıya kesme zoru veya germe zoru uygulanamaz (o gerçek bir akışkandır).
Bu yazımızda sizlere katıların esneklik özellikleri hakkında bilgi verdik. Diğer yazımızda görüşmek üzere.