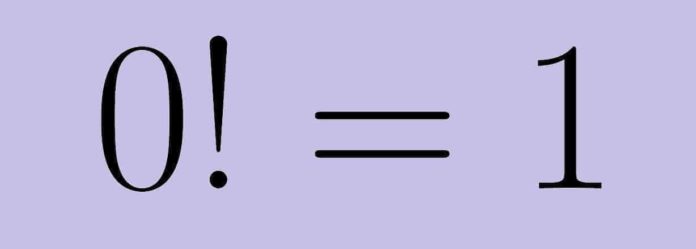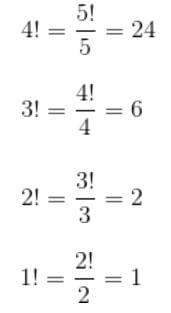0!=1 mi? Neden? Çocukluktan beri öğretilen 0!=1 olduğu kanısının nereden geldiğini merak etmişsinizdir. Faktöriyel konusunun önemli bir parçasını oluşturan bu ince kuralı inceleyelim.
Matematikçiler ve öğrenciler için faktöriyel konusu çok farklı yollarla hesaplanmaktadır. İkisi de doğru fakat öğrencilerin yaptığı hareketler ya da işlemler daha kısa ve zaman açısından basit hale getirmektedir.
n! = n. (n-1) . (n-2) . ….. .. … . 1
şeklinde hesaplanmaktadır. Yani genel olarak da ” Bir sayıdan 1 eksilterek çarpılması durumuna faktöriyel denilmektedir. ” Peki yukarıda ki formülü direkt kullanarak 0!’i bulabilir misiniz? Yani normal bir mantık çerçevesinde,
0! = 0. ( 0-1 ) . (0-2)…….?
şeklinde tanıma uymayan bir matematiksel hal ile karşılarız. Bu hata ise asıl faktöriyel kavramının amacından çıkmasından yani daha iyi yorumlaması için düzenlenen tanımından kaynaklanmaktadır.
Peki faktöriyel kavramının asıl tanımı nasıl? Bu kavram ilk olarak 18 yy. Fransız matematikçi Louis Arbogast tarafından ilk temelleri atılmış, daha sonraları De Moivre, Euler ve Christian Kramp tarafından da ele alınmıştır. İlk tanım şu şekildeydi;
şeklinde tanımlanmıştı. Bakın burada hemen, 0! ifadesini bulabiliriz. Bunun için 1!’in kaç olduğunu bulmamız gerekiyor. İlk tanıma göre,
5!= 5.4.3.2.1= 120 olduğundan,
olacaktır. Burada hemen 1!=1 olduğunu gördük, gelelim 0! meselesine. Aynı biçimde,
olacaktır. İşte 0!=1 durumu buradan gelmektedir. Eskiden her zaman karıştırdığımız bir durum aslında matematiği ezberlemenin, altyapısının ne olduğunu sezememekten kaynaklanmaktır. Aslında bu araştırmayı burada bitirmek gerekiyordu fakat şunlardan da bahsedelim. Neden -1!, -2! ya da negatif faktöriyel ifadesi yok. Hemen aynı fikirden hesaplama yapalım,
olacağından ve 0! = 1 olduğunu da bildiğimizden
olacağından bu bize bir tanımsızlık verecektir. Aynı biçimde -1! tanımlanamadığı için bir zincir misali diğer negatif faktöriyeller de bulunamayacaktır. Harika…
Referans
- numberphile/youtube