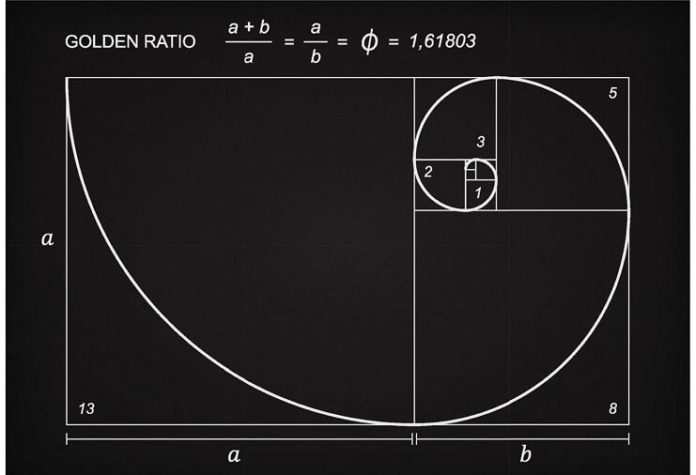
Altın Oran ya da İngilizce olarak çok sık duyduğumuz “Golden Ratio” aslında matematiğin doğaya yansımasıdır. Estetik güzellik ve mutlak güzellik kavramlarının bir sanatçıya göre matematiksiz olamayacağını gösteren bir oran. Bu araştırmada aslında altın oran meselesinin doğada nerelerde bulunduğundan çok matematiksel olarak çıkış noktasının nasıl gerçekleştiğini konuşacağız.
Altın oran ilk olarak eski Yunanlılar tarafından incelenmiş ve geometri açısından tanımlanmıştır. Bir parça çizgi alın ve daha uzun ve daha kısa bir parça halinde bölün. Böylece, bütün parça ile uzun parça arasındaki oran, uzun parça ile daha kısa parça arasındaki oran ile aynı olur.
Bu oran için phi yazalım. Phi değerini oldukça kolay bir şekilde hesaplayabiliriz. Bölmeden sonra uzun çizgi parçasının uzunluğu a ve kısa olanın b uzunluğuna sahip olduğunu varsayalım. Sonra, phi , tüm satırla a arasındaki oran ve aynı zamanda a ile b arasındaki oranı eşittir
 Bu oran için phi yazalım. Phi değerini oldukça kolay bir şekilde hesaplayabiliriz. Bölmeden sonra uzun çizgi parçasının uzunluğu a ve kısa olanın b uzunluğuna sahip olduğunu varsayalım. Sonra, phi tüm satırla a arasındaki oran ve aynı zamanda a ile b arasındaki oranı eşittir. Aynen şu şekilde,
Bu oran için phi yazalım. Phi değerini oldukça kolay bir şekilde hesaplayabiliriz. Bölmeden sonra uzun çizgi parçasının uzunluğu a ve kısa olanın b uzunluğuna sahip olduğunu varsayalım. Sonra, phi tüm satırla a arasındaki oran ve aynı zamanda a ile b arasındaki oranı eşittir. Aynen şu şekilde,
![]()
Denklemin sol tarafı şu şekilde yazılabilir:
![]()
olur ve bunu aynı yerine yazabiliriz.
![]() Dolayısıyla elde edeceğimiz denklem şu şekildedir. Bu noktadan sonra altın oran meselesinin matematiksel olarak ne anlatmak istediğini sezeceğiz.
Dolayısıyla elde edeceğimiz denklem şu şekildedir. Bu noktadan sonra altın oran meselesinin matematiksel olarak ne anlatmak istediğini sezeceğiz.
![]()
Şimdi her terimi yani eşitliğin her iki tarafını phi ile çarpalım ve elde ettiğimiz denklemi yazalım.
![]()
Bu bir quadratic denklem yani ikinci dereceden bir bilinmeyenli. Bu tip denklemleri gözümüz kapalı olarak lise bilgilerim ile yapabiliriz. Denklemin kökü ya da çözüm kümesi;
![]()
olacaktır. İlk kısım matematikçiler ve fizikçiler tarafından yaygın olarak bilinirken sayısalısım hemen hemen altın oran kelimesini duyan kişilerin bildiği kısımdır. Asıl çıkış noktası bu şekilde olsa da bir de “ Fibonacci Dizisi “ ile hesaplan bir başka biçimi vardır.
Altın oran her türlü ilginç özelliklere sahip, ancak belki de en ünlü olanı Fibonacci dizisine olan bağı.
Bu ünlü numaralar dizisi iki nokta ile başlar. Sonraki sayılar, önceki iki sayı eklenerek oluşturulur. Aynen şöyle,
![]()
Dizilim süresiz olarak devam edebilir. Fibonacci dizisindeki her bir sayıyı, önceden gelen sayıya bölerek yeni bir sıralama oluşturabilirsiniz.
Sırayı aşağı doğru taşırken sayıları sınırlayıcı bir değere yaklaştığını görebilirsiniz. Ve bu sınırlayıcı değer tam altın oranıdır!
Fibonacci dizisi ve altın oranı, doğadaki görünüşleri ve estetikle bağlantılı olması da dahil olmak üzere tüm oluşumlar matematiğin doğası adlı çalışmada bulabilirsiniz.