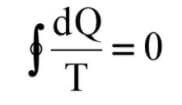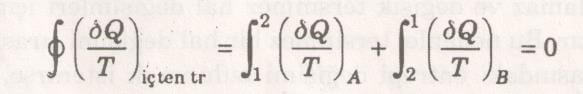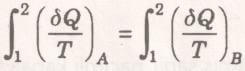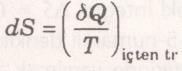Bir önceki yazılarda açıklanan clapeyron denklemi entropi adı verilen yeni bir özeliğin tanımı için temel oluşturmaktadır. Entropiyi tanımlayacak bir bağıntıyı geliştirebilmek için, aşağıdaki denklemi daha yakından inceleyelim. Bu bağıntıda çevrim üzerinde integrali sıfır olan bir büyüklük yer almaktadır. Bir an için hangi tür büyüklüklerin çevrim boyunca integrallerinin sıfır olduğunu düşünelim. işin çevrim üzerinde integralinin sıfır olmadığı bilinmektedir. İyi ki de bu böyledir, yoksa bir çevrim gerçekleştirerek çalışan buhar santrali gibi ısı makineleri net iş üretemezlerdi.
Isı geçişinin de çevrim üzerinde integrali sıfır değildir.
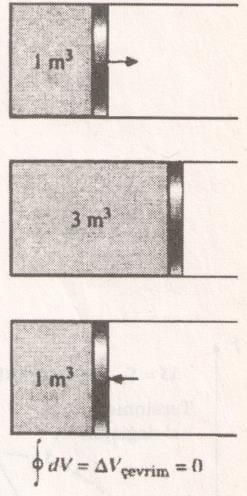
Şekilde gösterildiği gibi bir piston silindir düzeneğinde bulunan gazın kapladığı hacim göz önüne alınsın. Sistem bir çevrim gerçekleştirsin. Çevrim sonunda piston ilk haldeki konumuna döndüğü zaman, gazın hacmi de ilk haldeki değerini alacaktır. Böylece hacmin çevrim sonunda net değişimi sıfırdır. Bu düşünce matematiksel olarak gösterilirse, ∫dV=0 elde edilir. Başka bir deyişle, hacmin (veya herhangi bir özeliğin) çevrim üzerinde integrali sıfırdır. Benzer biçimde, çevrim üzerinde integrali sıfır olan bir büyüklük sadece hale bağlıdır ve hal değişiminin izlediği yoldan bağımsızdır, bu nedenle de bir özeliktir. Böylece (dQ/T) bir özeliğin diferansiyel biçimde yazılışı olmalıdır.
Bu konuyu daha iyi açıklayabilmek için, A ve B ile gösterilecek iki içten tersinir hal değişiminden oluşan bir çevrim incelensin. Denklem bu içten tersinir çevrime uygulanırsa,
elde edilir. İkinci integralin sınırlan ters çevrilir ve eşdeğerliliği sağlamak için integralin işareti değiştirilirse,
bulunur. A ve B, 1 ve 2 halleri arasında herhangi iki içten tersinir hal değişimi olduğuna göre, integralin değeri izlenen yola değil sadece ilk ve son hallere bağlı olacaktır. Bu nedenle yukarıdaki integral bir özelikteki değişimi gösterir. Clausius 1865’te yeni bir termodinamik özelik bulduğunu anlamış ve bu özeliğe entropi adını vermiştir. Entropi S simgesiyle gösterilir ve aşağıdaki gibi tanımlanır:
Dikkat edilirse, yukarıda tanımlanan entropi değil, entropi değişimidir. Benzer olarak kapalı bir sistem için birinci yasa bağıntısı çıkarılırken, enerji değil, enerji değişimi tanımlanmıştı. Entropinin mutlak değerleri bu yazıda daha sonra incelenecek olan termodinamiğin üçüncü yasasına dayanarak belirlenecektir. Mühendisler genellikle entropi değişimleriyle ilgilenirler. Bu nedenle bir maddenin entropisi herhangi bir referans halinde sıfır kabul edilip, diğer hallerdeki entropi değerleri bu hale göre belirlenebilir. Bu durumda denklemde, 1 hali referans halini, 2 hali de entropinin bulunmak istendiği hali gösterecektir.
Yukarıdaki denklemdeki integrasyonu yapmak için hal değişimi sırasında Q ile T arasındaki ilişkiyi bilmek gereklidir. Bu ilişki genellikle bilinmediği için denklemde gösterilen integrasyon sadece bazı hal değişimleri için yapılabilir. Entropinin belirlenmesi için büyük çoğunlukla tablolara başvurulur.
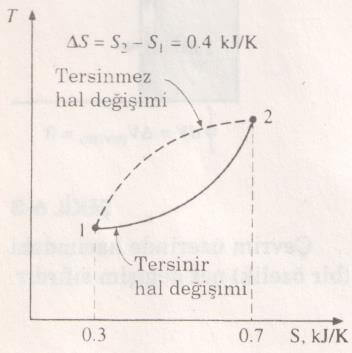
Entropinin bir özelik olduğu vurgulanmalıdır. Entropi de, tüm diğer özelikler gibi belirli hallerde belirli değerler alır. Bu nedenle iki hal arasındaki entropi değişimi AS, hal değişimi sırasında izlenen yola bağlı değildir.
dQ/T’nin integrali, iki hal arasındaki entropi değişimini ancak integral bu iki hal arasında içten tersinir bir hal değişimi üzerinde alınırsa verir. Tersinmez bir hal değişimi sırasında dQ/T’nin integrali bir özeliği tanımlamaz ve değişik tersinmez hal değişimleri için farklı değerler alacaktır. Bu nedenle, tersinmez bir hal değişimi sırasında, ilk ve son haller arasındaki entropi değişimi bulunmak istenirse, bu iki hal arasında tersinir bir hal değişimi tasarlayıp integrali bu hal değişimi üzerinde almak gerekir.