Tüm bilim ve mühendislik meraklılarına selamlar. Bu makale, akışkanlar mekaniği ve termodinamik prensipler ile yakından alakalı hemen hemen tüm sistemlerde kullanılan bir terim olan kütlesel debinin teorisi, çıkış noktası üzerine olacaktır. Bazı formüllerin nereden geldiği ile ilgilenerek onları türetmek, bazı kimseler için yeterince ilgi çekici ve faydalı gözükmeyebilir, fakat araştırma-geliştirme pozisyonlarında görev almak isteyen biz mühendisler için çok sık kullandığımız bazı kavramların nasıl türetildiğini bilmek, vizyon geliştirici niteliğe sahiptir.
Bilindiği gibi akışkanlar mekaniği yoğun bir şekilde tümevarım formüllerinden müteşekkildir. Kalkülüs (calculus) matematiğinin temelinde de sonsuz küçüklükteki değişkenlerin, integral yöntemi ile toplamının bulunması vardır. Bizde bu makalede aynı doğrultuyu kullanarak formülü elde etmeye çalışacağız.
Açıklamaya başlamadan önce vurgulamak istediğim bir durum var. Reynolds sayısı, bir akışın laminer veya türbülanslı olduğunu tayin etmek için kullanılan bir kriterdir. Reynold transport teoremi ile burada karıştırılmamalıdır, çünkü reynold transport teoremi burada anlatacağım bilgiden ziyade akışkanlar mekaniğinde lineer momentum denklemlerinde karşımıza çıkar. Laminer akış katmanlar halinde düzgün akan bir akış modelini tanımlarken, türbülanslı akış kaotik bir akışı temsil eder. Genel olarak dairesel bir geometri içerisinde(örneğin bir tüp/boru) akan iç akış için kritik Reynolds değeri 2300’dür ve bu değer referans alınarak akışın laminer olup olmadığına karar verilir. Reynolds sayısı aşağıdaki formülde de görülebileceği üzere, kuvvetlerin oranı olduğundan dolayı birimsiz/boyutsuzdur. Ek bir not olarak, Reynolds sayısının geometriler ve koşullar arasında farklılık gösterebildiğini de belirtmek isterim.
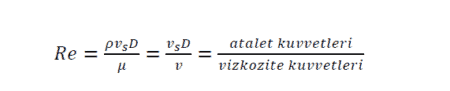
Bu açıklamadan sonra kütlesel debi formülüne bir göz atalım;
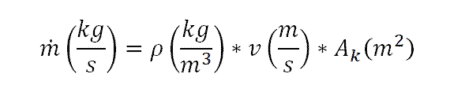
Kütlesel debi anlam olarak “birim zamanda belirli bir yüzeyden/geometriden akan kütle miktarı” olarak tanımlanır ve bu sebeple birimi kilogram/saniye ‘dir. Peki neden yoğunluk*hız*kesit alanı bağıntısını kullanırız?
Öncelikle bir adet kapaklı boru düşünelim ve kapağın şuan da kapalı olduğunu, eğer açılırsa akışın sol taraftan (kapağın arkasından) sağ tarafa doğru yönleneceğini hayal edelim. Sir Isaac Newton’un düşünce metodunu kullanalım ve tüm sistemi tasarlamak yerine, en küçük parçacıktan, yani bir adet su molekülünden yola çıkalım. Bu su molekülü, kapalı kapağın hemen yüzeyinde bekliyor olsun ve kapağı açtığımızda ilk önce bu molekülün harekete geçeceğini düşünelim.
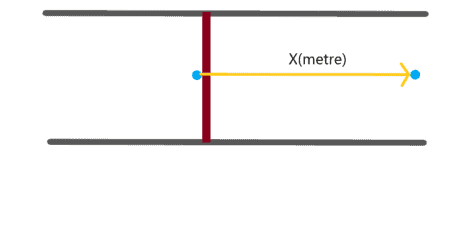
Bize verilen ortalama akış hızının x metre/saniye olduğunu varsayalım. Bu durumda kapak açıldıktan bir saniye sonra, bir su molekülü x metre yol alacaktır. Aynı şekilde ilk parçacığın bir saniye önceki konumuna, kapağın başlangıçta x metre solundaki bir parçacık yerleşmiş olacaktır.
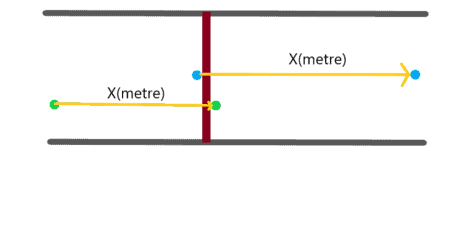
Bir saniye sonra kapak kapandığı anda akış kesilecektir ve kontrol hacmimize daha fazla molekülün girmesi engellenecektir. Artık kapağın sağ tarafında kalan moleküller ile ilgileneceğiz. Eğer dikkat ederseniz kapağın sağ tarafında en önde bir parçacık ve en solda bir parçacık kaldı. Bunların hacminin dv olduğunu belirtmiştik. Bu iki parçacık bizim kontrol hacmimizin sınırlarını belirlemektedir. Y ekseninde tüp yüzeyleri sistemi zaten sınırlamaktaydı ve an itibariyle en sağda bir parçacık (ondan daha ileride bir parçacık olamaz, çünkü ortalama hız kullanmaktayız) ve en solda bir parçacık sistemi x ekseninde de sınırlamış oldu. Bu iki adet sınır (boundary) parçacığı dışında arada da bir sürü parçacık yerleşmiş olacaktır.
Maddenin kütlesel yoğunluğu “birim hacim başına düşen kütle miktarı” olarak tanımlanır ve bu sebeple birimi kilogram/metreküp ‘tür. Bizim sistemimizde akışkanın kapladığı hacim V ise, biz
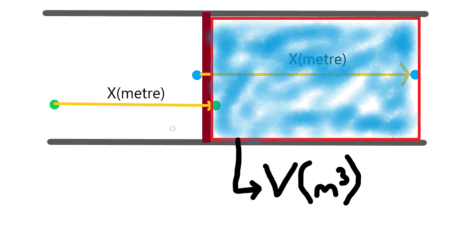
V = Ak(kesit alanı)*X(ilk parçacığın bir saniyede aldığı yol)
diyebiliriz. Şekil bu bağıntıyı tasdik etmektedir. Akışkanın kütlesel yoğunluğunu biliyorsak ve bizim sistemimizde de kapladığı hacim belli olduğuna göre,
Yoğunluk*Hacim(Akışkanın bir saniyede kapladığı hacim) = Kütle(Akışkanın bir saniyede kapladığı hacimdeki kütlesi)
Yoğunluk*(Ak*X) = Kütle(Akışkanın bir saniyede kapladığı hacimden yola çıkılarak elde edilmiş olan kütle)
X = Parçacığın bir saniyede aldığı yol = V(hız)(m/s)
olmaktadır. Bir üstteki bağıntıda, kapak açıldıktan bir saniye sonra akışkanın kapladığı hacimdeki kütleyi bulmuş olduk. Yani esasen bir saniyede akan akışkanın kütlesini bulmuş olduk ki, bunu da makalemizin konusu olan “kütlesel debi” dir.
Umarım makaleden keyif almışsınızdır, sevgi ve saygılarımla.


