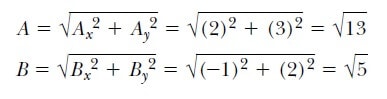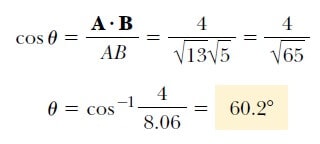Kuvvet ve yerdeğiştirme vektörlerinin eşitlik 1 şeklindeki yazılışı, vektörlerin skaler çarpımı olarak adlandırılan uygun bir matematik araç kullanmanın yararlı olacağını söyler. Bu araç, F ve d nin ne kadar birbirine paralel oluşuna bağlı olacak ve nasıl etkileştiğini gösterecektir. Bu skaler çarpımı F.d olarak yazarız. (Kullanılan nokta simgesinden dolayı, skaler çarpıma genellikle nokta çarpım da denir.) Bu durumda, 1 Eşitliğini bir skaler çarpım olarak ifade edebiliriz:
W = FdcosΘ ( Eşitlik 1)
W= F.d = FdcosΘ (Eşitlik 2)
Başka bir deyişle F.d (“ F nokta d ” olarak okunur) FdcosΘ ’nın kısaltılmış bir gösterimidir.
Genel olarak A ve B gibi herhangi vektörlerin skaler çarpımı, iki vektörün büyüklükleri ile bunların arasındaki açının kosinüsünün çarpımına eşit olan skaler bir niceliktir:
A.B = ABcosΘ (Eşitlik 3)
Bu bağıntı Şekil 1’de gösterilmiştir. A ve B nin aynı birimlere sahip olması gerekmediğine dikkat ediniz.
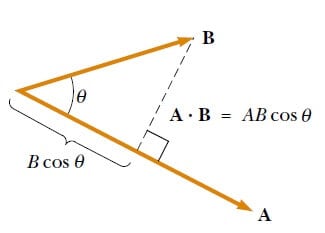
Şekil 1 ‘de BcosΘ, B’nin A üzerindeki izdüşümüdür. O halde 3. Eşitliğe göre A.B, A ‘nın büyüklüğüyle, B nin A üzerindeki izdüşümünün çarpımını ifade eder.
3 Eşitliğinin sağ tarafından, aynı zamanda skaler çarpımın yerdeğiştirebilir (komutatif) olduğunuda görüyoruz. Yani,
A.B = B.A
dır.
Son olarak vektörlerin skaler çarpımı,
A.(B + C) = A.B + A.C
olacak şekilde çarpmanın dağılma yasasına da uyar.
A, B’ye dik veya paralel olduğunda, 3 Eşitliğinden nokta çarpımı hesaplamak kolaydır. A, B’ye dikse (Θ = 90°), A.B = 0 olur. (A.B = 0 eşitliği aynı zamanda A, ya da B nin sıfır olması durumunda da sağlanacağı açıktır.) A vektörü, B vektörüne paralel ve aynı yönlü iseler A.B = AB dir. A vektörü B vektörüne paralel fakat ters yönlü iseler (Θ = 180°), A.B = – ABdir. 90° < 0 < 180° olduğunda skaler çarpım negatiftir.
i, j, k birim vektörleri, bir sağ koordinat sisteminin sırasıyla pozitif x,y ve z eksenlerinde yeralır. Dolayısıyla A.B nin tanımından bu birim vektörlerin skaler çarpımları
i.i = j.j = k.k = 1 (Eşitlik 4)
i.j = i.k = j.k = 0 (Eşitlik 5)
dir. A ve B vektörlerinin, bileşenleri cinsinden
A = Axj + Ayj + Azk
B = Bxi + Byj + Bzk
biçiminde de ifade edilebileceğini söyler. 4 ve 5 Eşitliklerinde verilen bilgi, A ile B nin skaler çarpımının
A.B = AxBx + AyBy + AzBz
ya indirgenebileceğim gösterir. A = B olan özel durumda
A.A = Ax2 + Ay2 + Az2 = A2
olacağı anlaşılır.
Vektörlerin Skaler Çarpımı İle İlgili Örnek
Örnek: A ve B vektörleri, A = 2i + 3j ve B = – i + 2j olarak veriliyor,
(a) A.B skaler çarpımını hesaplayınız.
(b) A ile B arasındaki Θ açısını bulunuz.
Çözüm:
(a) A.B = (2i + 3j).(-i + 2j)
=- 2i.i + 2i.2j – 3j.i + 3j.2j
= -2(1) + 4(0) – 3(0) + 6(1)
= – 2 + 6 = 4
Burada i.i = j.j = 1 ve i.j = j.i = 0 olduğu gerçeğini kullandık. 7.9 Eşitliğini kullandığımızda aynı sonuç elde edilir. Burada Ax = 2, Ay = 3, Bx = – 1 ve By = 2 dir.
(b) A ve B nin büyüklükleri şöyledir:
3.Eşitliğe ve (a) şıkkının sonucunu kullanarak
buluruz.