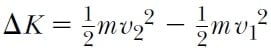Merhaba arkadaşlar bu yazımızda sizlere bernoulli denklemi nedir, bernoulli ilkesi ve bernoulli denklemi uygulamalarını sizlere anlatacağım. Bir bahçe hortumundaki suyun çıkış ucu baş parmakla sıkıştırıldığı zaman, çıkış deliği daralır ve su yüksek hızla dışarıya çıkar. Su hortum içinde mi yoksa havada olduğu zaman mı daha büyük basınç altındadır? Bu soruya, başparmağınızla hortum içindeki suyu nasıl zorla sıkıştırdığınıza dikkat ederek, cevap verebilirsiniz. Hortumun içindeki basınç, kesinlikle atmosfer basıncından daha büyüktür.
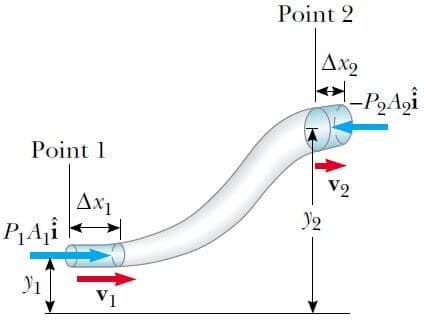
1738 de; İsviçreli fizikçi Daniel Bernoulli (1700 – 1782), ilk kez basıncı, akışkanın hızına ve yüksekliğine bağlayan ifadeyi türetti. Şekil 1 de gösterildiği gibi t süresinde değişik kesitli boru içindeki akışkanı ele alalım. Akışkanın alt ucundaki kuvvet P1A1, olur. Burada P1 , 1 konumundaki basınçtır. Bu kuvvetin t süresince yaptığı iş W1 = F1Δx1 = P1A1Δx1 olur. Burada; V, borunun alt kısmındaki bölgenin hacmidir. Benzer şekilde, t zamanında borunun üst ucundaki akışkanın aynı t süresince yapmış olduğu iş W2 = -P2A2Δx2 = -P2V olarak bulunur. (Aynı zaman aralığında 1 ve 2 konumlarından geçen sıvının hacmi aynı olur.) Akışkanın kuvveti yer değiştirmeye karşı olduğu için bu iş negatiftir. Bu kuvvetler tarafından t süresinde yapılan net iş,
W= (P1-P2) V
olur. Bu işin bir kısmı, akışkanın kinetik enerjisini değiştirir, bir kısmı da çekim potansiyel enerjisine harcanır, t süresinde bir uçtan girip diğer uçtan çıkan kütle m ise kinetik enerjideki değişme,
şeklindedir. Potansiyel enerjideki değişme de
ΔU = mgy2 – mgy1
olur. W= ΔK+ ΔU iş-enerji teoremini akışkanın bu hacmine uyguladığımızda,
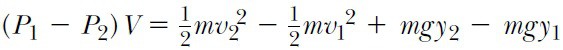
elde edilir. Her terimi V ile bölersek ve ρ = m/ΔV alırsak, yukardaki ifade
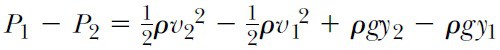
şekline gelir. Terimleri yeniden düzenleyerek,
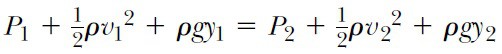
elde edilir. Bu, kararlı durumdaki vizkoz olmayan ve sıkışmayan akışkana uygulanan Bernoulli Denklemidir. Bu denklem genellikle,
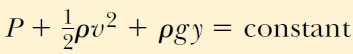
şeklinde ifade edilir. Bernoulli denklemi, basınç (P), birim hacim başına kinetik enerji (1/2ρv) ve birim hacim başına potansiyel enerji (ρgy) nin toplamının akış çizgisi üzerindeki bütün noktalarda aynı değere sahip olduğunu ifade eder.
Akışkan durgun ise vl = v2 = 0 olduğundan
P1 – P2 = ρg(y2 – y1) = ρgh
olur.
Bernoulli Denklemi Uygulamaları
Uçak kanadına etki eden kaldırma kuvveti, kısmen, Bernoulli denklemi ile açıklanabilir. Uçakların kanatlarının tasarımı, kanat üzerindeki hava hızı, kanat altındaki hızdan daha büyük olacak şekilde yapılır. Sonuçta, kanat üstündeki basınç, kanat altındaki basınçtan daha küçük olur ve kaldırıcı kuvveti denilen yukarıya doğru net bir kuvvet ortaya çıkar.
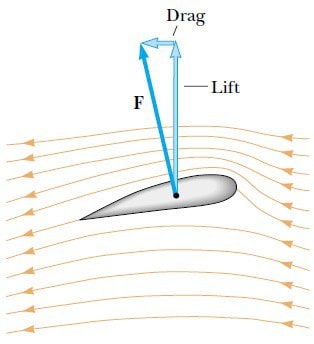
Kanat üzerindeki kaldırıcı kuvveti etkileyen başka bir etken Şekil 2’te görülmektedir. Uçak kanatlarının biçimleri, üst yüzeyinin eğrilik yarıçapı alt yüzeyinden daha küçük olacak şekilde dizayn edilir. Üst yüzeyden geçen hava akımı, alt yüzeyden geçen hava akımından daha eğrilmiş olarak akar. Azalan basıncın yönü eğrilik merkezine doğru olduğundan basınç üst yüzeyde daha azdır. Yaklaşan hava, bu alçak basınç bölgesine doğru ivmelenir; böylece, hava üst yüzeyde daha hızlı olarak geçer. Kanat üzerinde oluşan bu bileşke kuvvete dinamik kaldırma kuvveti adı verilir. Bu kuvvet, uçağın hızı, kanadın alanı, eğriliği, kanadın yatayla yaptığı açı ve eğimi gibi pek çok faktöre bağlıdır. Bu açı artarken, kanadın üzerindeki girdaplı akış, Bernoulli prensibiyle oluşan kaldırma kuvvetini azaltır. Pratikte kanatlar, genellikle yukarıya doğru eğimli olarak yapılır. Bu durumda, kanadın altındaki hava kütlesi, kanadın aşağıya sapmasını önler. Kanadın alt yüzeyine çarpan hava akımı kanatta yukarıya doğru ek bir kuvvetin oluşmasına neden olur (Newton’un üçüncü yasası).
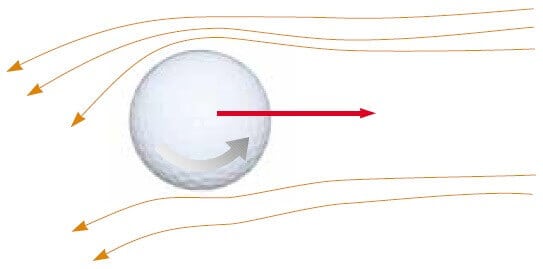
Genellikle, akışkan içinde hareket eden bir cisim bir kaldırma (kaldırıcı) kuvvetinin etkisinde kalır. Bu kuvvet, akışkan cismi geçip giderken doğrultusunu değiştirmesi sonucu ortaya çıkar. Cismin biçimi, akışkanın akışına göre konumu, yaptığı spin hareketi ve cismin yüzeyinin yapısı gibi etkenler kaldırıcı kuvveti etkiler. Örneğin; bir sopa ile vurulan bir golf topu, çok hızlı geriye doğru bir dönme hareketi yapar. Top üzerinde ki çukurlu yüzeyler, havanın top yüzeyinin eğriliğini izlemesine yardım eder. Bu olay, hava akımıyla aynı yönde hareket eden top yüzeyinin üst yarı kısmında daha çok görülür. Şekil 3, topun çevresini saran ince hava tabakası ve sonuçta havanın aşağıya doğru sapmasını gösterir. Çünkü top, havayı aşağıya doğru ittiği için hava da topu yukarıya doğru itmelidir. Çukursuz yüzeylerde hava girişi iyi olmaz ve golf topu uzağa gidemez. Aynı nedenle, tüylü bir tenis topu, hızlı havayı yakalar ve dönme hareketine yardım eder ve onun sapmasını sağlar.
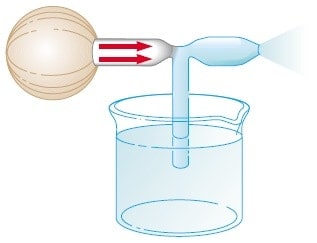
Pek çok düzenek, bir akışkanın hızındaki farktan ortaya çıkan basınç yardımıyla çalışmaktadır. Örneğin; Şekil 4’te görüldüğü gibi, bir ucu sıvıya daldırılan ve diğer açık ucu üzerinden hava akımı geçirildiğinde, tüpün üst ucundaki hava basıncı azalır. Basınçtaki bu azalma, sıvının hava akımının içine doğru yükselmesine neden olur. Böylece, sıvı ince damlalar halinde dışarıya fışkırır. Boya ve parfüm püskürtücüleri olarak kullanılan ve atomizer adı verilen düzenekleri hatırlarsınız. Aynı prensip, benzin motorlarının karbüratöründe de kullanılır. Bu durumda, karbüratördeki alçak basınç bölgesi, hava filtresi pistonu ile çekilen hava ile oluşturulur. Benzin, buharlaştırılır ve hava ile karıştırılır, sonra sıkıştırmak için motorun silindirine gönderilir.