Bu yazımızda dirençli ortamlarda hareketi ele alacağız. Şimdiye kadar cismin hareketi süresince cisim ile içinde ilerlediği ortam arasındaki etkileşmeler tamamen gözardı edildi. Şimdi gaz veya sıvı olabilen ortamın hareketli cisme etkilerini ele alalım. Bir ortam, içerisinde hareket eden cisme R direnç kuvveti uygular. Hareketli kamyonlara hava tarafından uygulanan direnç ve bir sıvı içinde hareket eden cisme etki eden vizkozluk kuvveti bazı örneklerdir. R nin büyüklüğü cismin sürati gibi bazı faktörlere bağlıdır ve yönü cismin ortama göre yaptığı harekete tersdir. R’nin büyüklüğü daima hız arttıkça artar.
Genel halde, direnç kuvvetinin hıza bağlılığı çok karmaşıktır. Aşağıdaki tartışmada iki durum göz önüne alınacaktır. Birinci durum, direnç kuvvetinin hız ile orantılı olduğunun kabulüdür; bir sıvı içinde düşen cisimler ve hava içinde hareket eden toz gibi küçük parçacıklar, bu tür direnç kuvvetlerinin etkisindedirler. İkinci durum, direnç kuvvetinin hareketli cismin hızının karesi ile orantılı olduğu olaylardır; uçaktan atlayan hava dalgıçları gibi büyük cisimler, çekim kuvveti etkisiyle serbest düşme yaparken hızın karesi ile orantılı direnç kuvvetinin etkisinde kalırlar.
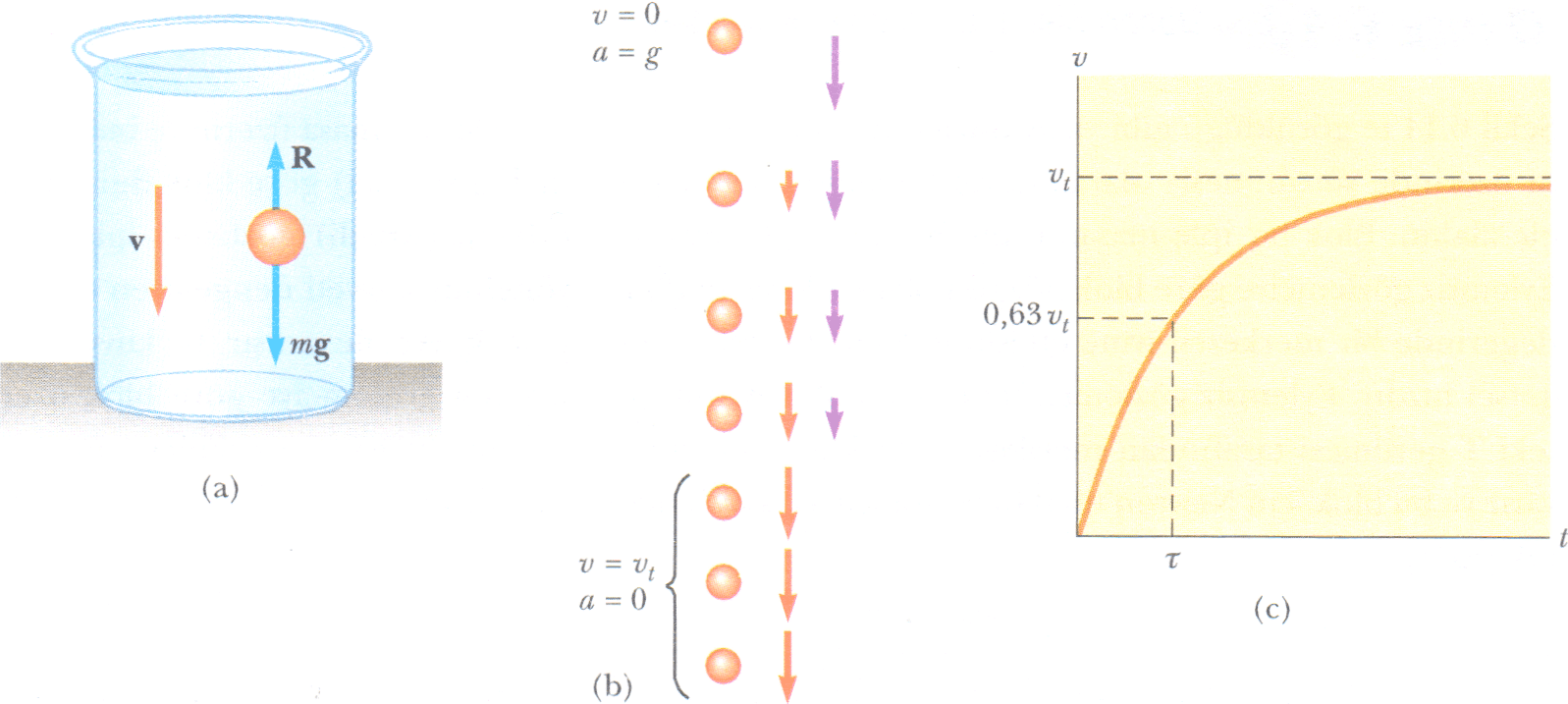
Hız İle Orantılı Direnç Kuvveti
Bir cisim sıvı veya gaz ortam içinde hareket ettiği zaman, cismin hızı ile orantılı olan bir durdurucu direnç kuvveti etkisinde kalır. Bu direnç kuvvetinin büyüklüğü aşağıdaki gibi ifade edilebilir.
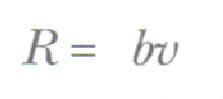
Burada v, cismin hızı, b de ortamın özelliklerine, cismin boyutlarına ve şekline bağlı bir katsayıdır. Cisim, r yarıçaplı bir küre ise, o zaman b katsayısı rile orantılıdır.
Şekil 1 a’da görüldüğü gibi m kütleli r yarıçaplı bir cismin durgun halden bir akışkan içinde serbest bırakıldığı hali inceleyelim. Cisim üzerine etki eden kuvvetlerin sadece bv direnç kuvveti ile F çekim kuvvetinden ibaret olduğunu farz ederek, cismin hareketini tasvir edelim. Aşağı doğru yönü pozitif olarak seçip, düşey doğrultuda Newton’un ikinci yasasını uygulayarak ΣFy= mg-bv olduğuna dikkat edersek aşağıdaki eşitlik yazılabilir.
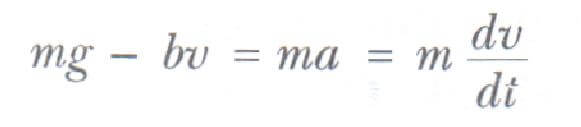
Burada dv/ dt ivmesi aşağı doğrudur. Bu denklemden ivme ifadesi aşağıdaki gibi yazılabilir.
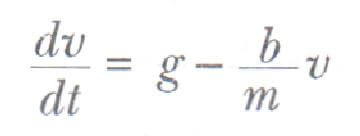
Hemen üstteki eşitlik bir diferansiyel denklemdir ve çözüm yolu henüz sizin için açık olmayabilir ancak, başlangıçta v = 0 olduğu zaman direnç kuvvetinin sıfır ve dv/dt ivmesinin de g çekim ivmesine eşit olduğuna dikkat ediniz. t zamanı arttıkça direnç kuvveti de artar ve ivme azalır. Sonunda direnç kuvveti ağırlığa eşit olunca ivme sıfır olur. Bu noktadan itibaren cisim sıfır ivme ile yoluna devam eder ve vt ile gösterilen bir limit hıza ulaşır. Limit hız aşağıdaki gibi elde edilir.

v = 0 ve t = 0 durumunda hız ifadesi aşağıdaki gibi olur:
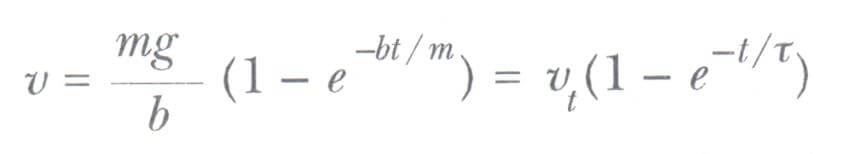
Bu fonksiyonun grafiği Şekil 1 c’de çizilmiştir. Zaman sabiti т = m/b’dir. Bu, hızın ( v’nin) 0,632vt = (1 – 1/e) değerine ulaşması için geçen zamandır. bir üstteki eşitlikte t = т konulunca v = 0,632 Vt olduğu görülebilir.
Üstteki son iki denkleme ait bir çözüm olup olmadığını doğrudan diferansiyelini alarak kontrol edebiliriz.
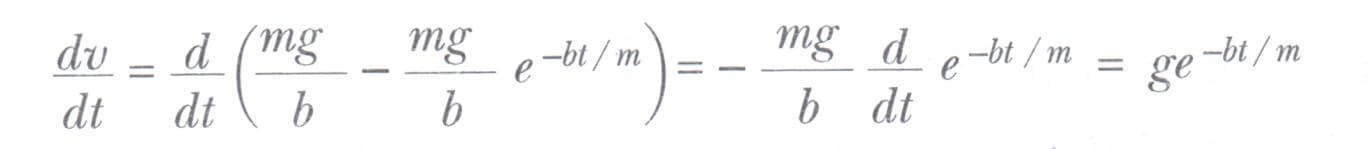
Yüksek Hızlarda Hava Direnci
Hava içerisinde çok büyük hızla hareket eden ve büyük boyutlu cisimler, örneğin uçaklar, hava dalgıçları, beyzbol topu gibi cisimler için direnç kuvveti yaklaşık olarak hızın karesi ile orantılıdır. Bu durumda direnç kuvveti aşağıdaki gibi ifade edilebilir.
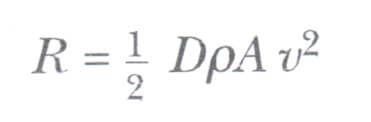
Burada p havanın yoğunluğu; A düşen cismin hareketine dik doğrultudaki yüzeyine karşı gelen alandır. D direnç katsayısı olarak adlandırılan boyutsuz bir katsayı’dır. Bu direnç katsayısı küresel cisimler için yaklaşık olarak 0,5 değerine sahiptir. Fakat düzensiz şekilli cisimler için 2 değerine kadar yükselir.
Şimdi yukarı doğru R = 0.5DpAv^2 ile verilen hava direnci etkisinde serbest düşme yapan bir kütlenin hareketini inceleyelim. Bir m kütleli cisim Şekil 2’de görüldüğü gibi у = 0 konumunda durgun halden serbest bırakılsın. Kütle iki dış kuvvet etkisinde kalır. Bunlar aşağı doğru olan Fg= mg çekim kuvveti ve yukarıya yönelmiş olan R direnç kuvvetidir. Ayrıca ihmal ettiğimiz yukarı doğru yönelmiş bir de kaldırma küveti vardır. Böylece etki eden net kuvvetin büyüklüğü aşağıdaki gibidir.
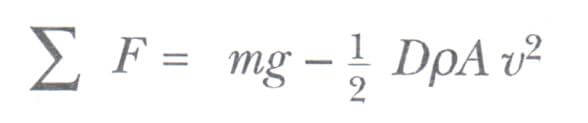
Burada aşağı yönü pozitif aldık Fnet =ma ifadesini bir üstteki eşitliğinde yerine koyarak kütlenin aşağı yönlü ivmesinin büyüklüğünü buluruz.
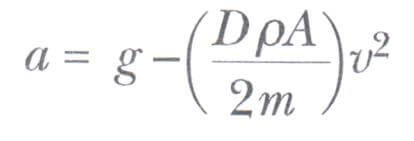
Limit hız ifadesini, direnç kuvvetinin ağırlığa eşit ve ivmenin sıfır olmasından aşağıdaki gibi elde ederiz. Bir üstteki eşitlikte a = 0 konularak ve v yi de vt alarak aşağıdaki ifade bulunur.
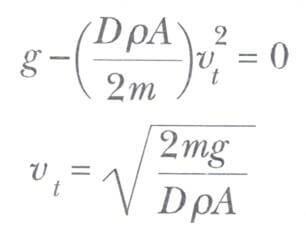
Bu ifadeyi kullanarak limit hızın, cismin boyutlarına nasıl bağlı olduğunu belirleyebiliriz. Cismin r yarıçaplı bir küre olduğunu varsayalım. Bu durumda A ∞ r^2 (A = nr^2den) ve m ∞ r^3’dür (kütle hacimle orantılı olduğu için çünkü V= 4/3 nr^3’dür). Böylece Vt ∞ r^0,5 olur. Yani r arttıkça Vt hızı, yarıçapın karekökü ile orantılı olarak artacaktır.


