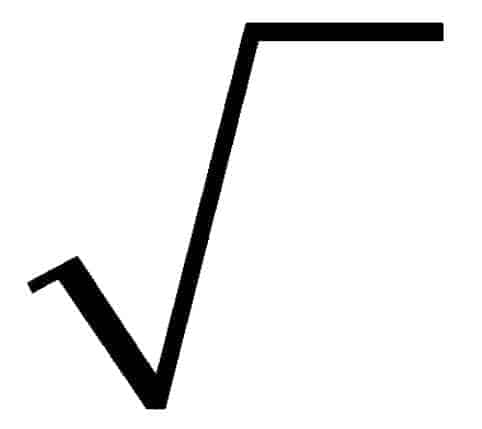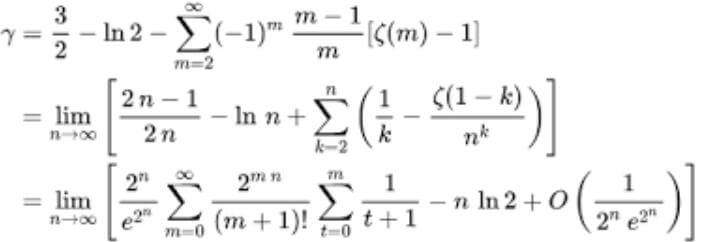Matematik içerdiği esrarengiz sabitlerle ve sayılarla insanların dikkatini çekmektedir. Hadi hazırsanız şimdi insanların daha doğrusu bilim insanlarının en önemli diye adlandırdığı bu sabitleri inceleyelim.
1-) 1 sayısı tüm zamanların en büyüleyicisi sayısı olarak ifade edilir. İnsanoğlunun ilkel zamanlarından itibaren bir çentik parçasıyla ifade edilen 1 sayısı tüm dinler ve felsefesi düşünceler içinde tekliği ve Tanrı’nın, yaratıcının birliğini simgelemektedir.
2-) 0 sayısı varlığı konusunda en çok şüpheye düşülen sayı olarak insanlar tarafından hissediliyor. İlk defa El- Harezmi tarafından ortaya atılan ve hiçlik yokluk sıfatlarının matematiksel karşılığı olarak bilinen 0 roma rakamlarında kullanılmayan tek sayıdır. Pozitifliği ve negatifliği iki gruba ayıran sıfır felsefelerde nötr durumunu simgeler.
3-) 7 sayısı tüm dinler için önemli yere sahiptir. 7 gün, yeryüzünün 7 katı, 7 kat gök, 7 kıta, 7 klasik gezegen, Hinduizm’in 7 hükümdarı, 7 ölümcül günah… Bazı matematikçilere göre 7 sayısı mükemmelliğin rakamı olarak gösterilir.
4-) √-1 (Kök -1) sayısı irrasyonel sayıların yani algıladığımız matematiksel bazların dışında gösterilen ilk sayı olarak kabul edilir. Reel kısımları olan tüm sayılara ek olarak kök -1 sayısında imajiner formlar gözükmektedir. Bu sayı matematik dünyasını alt üst etmiştir. i sayısı, her sabit olmayan polinom için en az bir kök verir. -1’in i ve –i olarak iki sanal karekökü bulunur.
5-) Euler sabiti ya da Euler-Mascheroni Sabiti, ϒ (gama) ile gösterilir ve matematiksel sabittir. Harmonik seri ile doğal algoritma arasındaki limit veya farktır. Sayısal değerinin ilk 10 basamağı: 0.5772156649
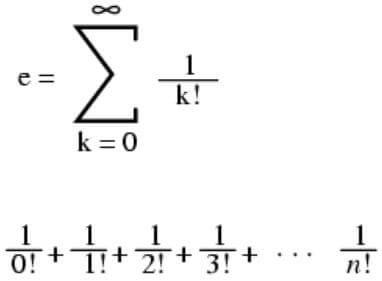
6-) Euler sayısı: Euler Sayısı ya da e sayısı, doğal logaritmanın tabanını ifade eder. Matematiğin yanı sıra doğa bilimleri, ekonomi ve mühendislikte de büyük öneme sahiptir. İrrasyonel bir sayı olan e sayısının yaklaşık değeri, 2.718’dir. İlk olarak John Napier tarafından kullanılmıştır. Sayıyı ilk keşfeden ve yaklaşık değerini hesaplayan, Jakob Benoulli’dir. İsmini verense, Leonhard Euler’dir. e sayısının irrasyonel bir sayı olduğu Euler tarafından, aşkın bir sayı olduğu ise, Charles Hermite tarafından kanıtlanmıştır.
7-) En Ünlü İrrasyonel Sayı: Arşimet Sabiti ya da Ludolph Sayısı olarak da bilinen Pi Sayısı, ismini, Yunanca çevre sözcüğünün ilk harfinden alır. Ondalıktan sonraki basamakları sonsuza dek uzanan pi sayısı (π / 3.14), bir dairenin çevresinin çapına bölümü ile elde edilen irrasyonel matematik sabitidir. Çok sayıda mimari ve geometrik problemin çözümünde kullanılır. Her yıl 14 Mart Pi Günü (3.14) olarak kutlanır.
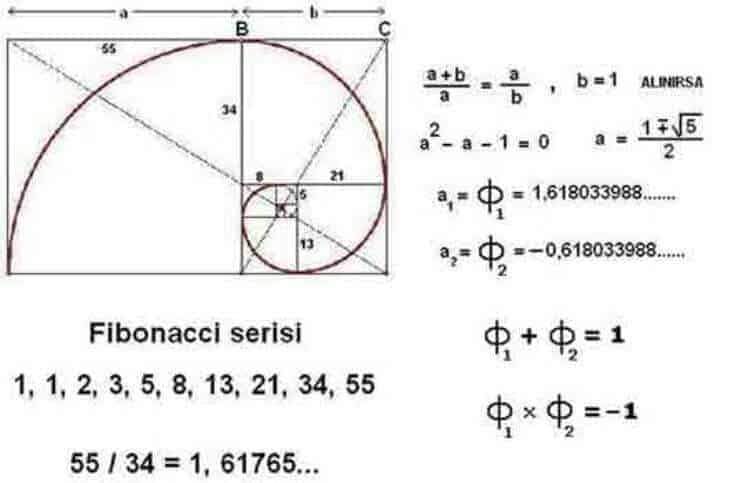
8-) Fibonacci Sayıları ve Altın Oran Fibonacci Sayıları (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …), Leonardo Fibonacci tarafından keşfedilmiştir. Fibonacci dizisinde ardışık iki sayının oranı, sayılar büyüdükçe Altın Oran’a yaklaşır. Altın Oran, tüm nesne ve varlıkların parçaları arasında bir uyum olduğunu saptar ve yaratıcının matematik sistemi olarak da isimlendirilir. Doğada, sanatta ve matematikte sıklıkla karşılaştığımız Altın Oran, yaklaşık 1.618’e denk gelen sabittir. Fi (Φ) sayısı ile gösterilir
9-) Planck Sabiti (h), kuantum mekaniğinde aksiyonun temel birimi olarak kabul edilen bir fizik sabitidir. Parçacıkların frekansı ile toplam enerjinin ilişkilendirilmesidir. Kuantum mekaniğine etki eden en küçük birim ya da süreksizliğin birimi olarak tanımlanabilir. Sabite, kuantum kuramını bulan bilim insanlarından biri olan Max Planck’in ismi sonradan verilmiştir.
10-) Işık Hızı 299792458 m/s yani ışığın boşluktaki hızı, dünyadaki en popüler sayılardan biri. Özellikle fizikte kullanılan önemli bir sabit olan ışık hızı, genellikle c ile gösteriliyor. Işık hızı, bir yıl içinde ışığın kat ettiği mesafeyi belirten ışık yılı teriminin temelini oluşturur. Görelilik Teorisinde ışık hızı, uzay-zaman arasındaki ilişkiyi kurar. Özel görelilik kuramına göre ışık hızı, evrendeki madde ve bilgilerin hareket edebileceği en yüksek hızdır.