Hayatın her alanında matematiğin uygulamasını görmek mümkün. Evrende her anın, her salisenin devam etmesini sağlayan yegane kuvvet enerjidir. Bir matematikçinin de en güzel yapacağı iş, enerjinin matematik ile olan ilişkisini belirlemektir. Euler özdeşliğini kullanarak enerji, volt ve amperler üzerinde bir iki teori üzerinde çalışalım.
A ve C uçları arasındaki voltajı hesaplamak için elektrik mühendisleri karmaşık sayılar kümesinin elemanı “i” olan karmaşık sayı kökünü kullanırlar.
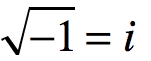
Bir kuadratik denklemde aslında hiçbir çözümünün bulunmadığı düşünülmektedir. Karmaşık sayılar ve bunların uzantısı kuadratik denklemi anlamlandırmak için 18. yüzyılda matematikçiler tarafından tanıtıldı ve başlangıçta muhtemel olmayan soyut matematiksel nesneler olduğu düşünülüyordu. Fakat daha sonraları birçok yerde uygulama alanı oluştu. Hele ki mühendisliğinin kalbinde bir gonca olmuştur.
Mühendisler akımdan geçen enerjinin birbiri ile karışmaması adına “i” ve “j” olmak üzere iki düzlemsel koordinatlardan farklı olarak yeni bir sistem gösterdiler. Matematik ile birlikte bu akımlar bir sisteme entegre edilmesi gerekiyordu bu işlem sonucunda da doğru hesaplamalar yapılması gerekiyordu. Her dakika, her saniye ve her salise… Bu iki kısım olan “i” ve “j” kısımları Euler özdeşliğine uygulandığında harika sonuçlar ortaya çıktı. Leonhard Euler zaten bu fikri savunan matematikçilerden biriydi fakat henüz kanıtını yapamamıştı. Ona göre Euler özdeşliği (Euler, bu özdeşliğe tanrı denklemi adını da vermiştir. Doğadaki tüm olaylar Euler özdeşliğinin izni olmadan gerçekleşmeyeceğini söylemiştir.) Şimdi unutanlar için şu Euler özdeşliğine tekrar bakalım. Matematiğin en önemli beş sabitini içeren bu denklem,
![]()
biçimindedir. Bakın burda Euler, enerjinin akımla olan ilişkisini tanımlamıştır. Aslında enerji bu denklemin bir fonksiyonudur.
![]() Bunu da düzenlersek, yani aynı tabanlara alırsak,
Bunu da düzenlersek, yani aynı tabanlara alırsak,
![]()
olacaktır. Yukarıda dediğimiz üzere, Euler özdeşliğinin bir fonksiyonu akım-volt özdeşliğidir. Yani, fonksiyondan değişkeni çekersek,
![]()
olacaktır. Bu ifade gerilimin genliğini ve fazı olmak üzere iki farklı değişken içerir.
Okuyucu için kısa not;
V(t) volt ve I(t) akım olmak üzere,
![]()
ve,
![]()
biçiminde ifade edilir. Belki bu noktada teknik bir bilgi daha vermek daha iyi olacaktır. φ’nin 50 Hz frekansa sahiptir. 1 ve 2 numaralar ise dalgaların fazladır. Faz, dalgaların yatay eksende ne kadar kaydırıldığını açıklar. Mutlak değer ifadesi olarak bulunan V ve I değerleri de dalgaların amplitüdleridir (Yükseklikleri).

