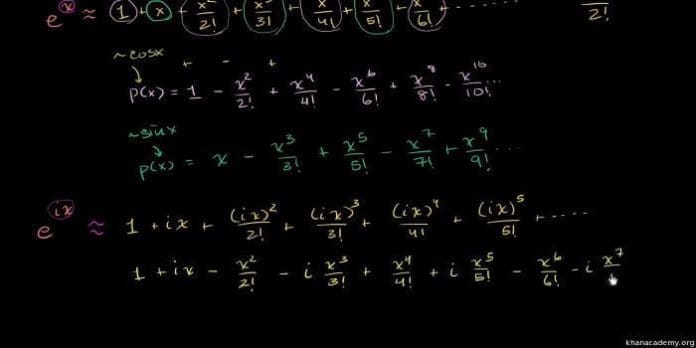Bu yazımda matematikteki en olağanüstü denkliklerden bir tanesi olan Euler özdeşliği hakkında bahsedeceğim. Yazımda yüzeysel ve temel olarak bilinen denkliklerden yararlanarak kainatın, olağanüstü sayıları bir araya getirip bir tam sayıya nasıl eşitlendiğini göstermeye çalışacağım. Bunun için Taylor serisi olarak bilinen seriye bakalım. Brook Taylor‘ın fonksiyonlarla oynayışı çok manidardır. Seriye göre bir fonksiyonda , fonksiyonun genelini kapsayan terimlerin bir tek noktasındaki türevinin değerlerinden hesaba gelen sonsuz toplamının yazılma şeklindeki açılımıdır. Formülize edersek;
F(x) = f(a) + (f'(a)/1!)(x-a) + (f”(a)/2!)(x-a)^2 + (f”'(a)/3!)(x-a)^3 + … ‘ dır. Bu fonksiyona Colin Maclaurin ismindeki matematikçi a=0 da bir bakış açısı getirerek daha basit bir biçime sokmuş ve Maclaurin serisini geliştirmiştir. Maclaurin serisinin matematiksel açılımı ;
F(x) = f(0) + f'(0)x + (f”(0)/2!)x^2 + … ‘ dir. Bunlardan istinaden şu denklemleri de vermek istiyorum.
Euler Özdeşliği Nedir
cosx’ in maclaurin serisi: 1- x^2/2! +x^4/4! – x^6/6! + …
sinx’ in maclaurin serisi : x – x^3/3! + x^5/5! – x^7/7! + …
e^x’ in maclaurin serisi 1+ x + x^2/2! + x^3/3! +x^4/4! + … ‘ dir.
Evet şimdi e^x ‘ in maclaurin serisindeki karşılığını ele alalım.
e^x = 1+ x+ x^2/2! + x^3/3! +x^4/4! + …
Bu denklikte x yerine ix yazalım ve çözümleyelim.
e^ix = 1+ ix + (ix)^2/2! + (ix)^3/3! + (ix)^4/4! + …
Şimdi biraz daha açalım.
e^ix= 1+ ix – x^2/2! – i(x^3)/3! + x^4/4! + i(x^5)/5! – x^6/6! – i(x^7)/7! + …
Reel ve imajiner kısımları bir araya toplayalım.
e^ix= (1 – x^2/2! + x^4/4! – x^6/6! + …) + i ( x -x^3/3! + x^5/5! – x^7/7! + …)
Yukarıda bazı değerlerin maclaurin serisine göre denkliklerini vermiştim. Görüldüğü üzere reel kısmın cosx ‘ in maclaurin serisine , imajiner kısmında sinx’ in maclaurin serisine denk gelmekte. Buna göre çok şık bir sonuç elde ederiz ve denklemimiz; e^ix= cosx + isinx olur.
Bence bu denklem matematiğin en büyük denklemleri arasında ilk 3 sırada yerini bulur. Şimdi işi biraz radyansal hesaba dökelim ve x yerine π yazalım. Denklemimiz : e^iπ = cosπ + isinπ olur. Lisedende bildiğimiz üzere cosπ = -1 ve sinπ = 0 dır. Yani denklemimiz : e^iπ= -1 olur. Toparlayacak olursak e^iπ + 1 = 0 denklemini elde ederiz. İşte bu denklem Euler denklemi olarak anılır. Bu denklem öyle bir güzellik taşır ki i’nin, π’nin ve e’nin kullanım alanlarının farklı olmasına rağmen evrenin, bu sayıların birleşiminin bir tam sayıya indirgediğini gösterir ve Euler, insanın hastalık düzeyine erişebilecek bu düzey matematik ilgisinin ne denli muhteşem bir bilgiye dönüşebileceğinin bir kanıtını da bu özdeşliğiyle gösterir…
Umarım anlaşılır bir yazı olmuştur. Okuduğunuz için teşekkür ederim.