Newton bir ağacın altında hafif bir uykuya dalmışken, düşen bir elmanın kafasına çarptığı şeklindeki efsaneyi duymuşsunuzdur. Bunun, Newton’u evrendeki bütün cisimlerin birbirlerini belki elmanın Dünya tarafından çekilmesinin aynısı olan bir yolla çektiğini düşünmeye sevk ettiği zannedilir. Newton, Ay’ın Dünya etrafındaki hareketine ait astronomik verileri çözümlemeye devam etti. Bu gibi verilerin çözümlenmesinden Newton, gezegenleri yöneten kuvvet yasasının yere düşmekte olan elmayı çeken kuvvet yasasıyla aynı matematik forma sahip olduğunu cesurca söyledi. Bununla ilk kez, “dünyasal” ve “gökyüzünde olan” hareketler birleştiriliyordu.
1687’de Newton, evrensel çekim yasası üzerine olan çalışmasını Doğal Bilimlerin Matematik İlkeleri adlı kitabında yayınladı. Newton’un evrensel kütle çekim yasası, “evrendeki her parçacık, başka bir parçacığı, kütlelerinin çarpımıyla doğru orantılı ve aralarındaki uzaklığın karesiyle ters orantılı olan bir kuvvetle çeker” şeklinde
ifade edilir. Eğer parçacıkların kütleleri m1 ve m2 ise ve birbirinden r gibi bir uzaklıkta bulunuyorlarsa, çekim kuvvetinin büyüklüğü aşağıdaki gibidir.
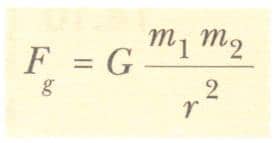
Burada G evrensel çekim sabiti denilen bir sabittir ve deneysel olarak ölçülmüştür.
SI birimlerindeki değeri:
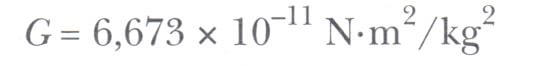
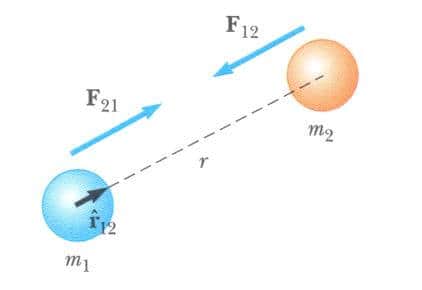
Eşitlik yukarıda verilen kuvvet yasasından çoğu zaman ters kare yasası olarak bahsedilir; çünkü kuvvetin büyüklüğü, parçacıkların arasındaki uzaklığın karesinin tersiyle orantılı olarak değişir. Bu tip kuvvet yasalarına uyan başka örnekleri gelecek bölümlerde inceleyeceğiz. Bu kuvveti, r12 gibi bir birim vektör tanımlayarak vektör biçiminde ifade edebiliriz. Bu birim vektör, m1 den m2 ye yönelmiş olduğundan, m2 üzerine m1 den dolayı etki eden kuvvet aşağıdaki formül ile verilir.
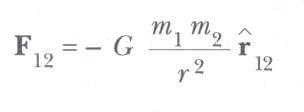
Eşitliğindeki eksi işareti, m2 nin m1’e çekildiğini gösterir. Bu yüzden kuvvet doğru yönelmiş olmalıdır. Benzer şekilde, Newton’un üçüncü kanunuyla m2 den dolayı m1 üzerine etki eden, F21 ile gösterilen kuvvet, büyüklük bakımından F12 ye eşittir ve zıt yöndedir. Yani bu kuvvetler bir etki tepki çifti oluştururlar ve F12 = -F21 dir.
Bir üstteki formülün biraz dikkat gerektiren birkaç özelliği vardır. Çekim kuvveti, parçacıkları ayıran ortamdan bağımsız olarak iki parçacık arasında daima var olan bir alan kuvvetidir. Kuvvet, parçacıklar arasındaki uzaklığın karesinin tersiyle orantılı bir şekilde değişir ve bu yüzden uzaklıkla arttıkça hızla azalır. Bir nokta kaynaktan çıkan ışığın şiddetinin, Aşağıdaki şekilde gösterildiği gibi, yine aynı 1/r^2 şeklinde azaldığına dikkat ederek, bu gerçeği durumun geometrisiyle bağdaştırabiliriz.
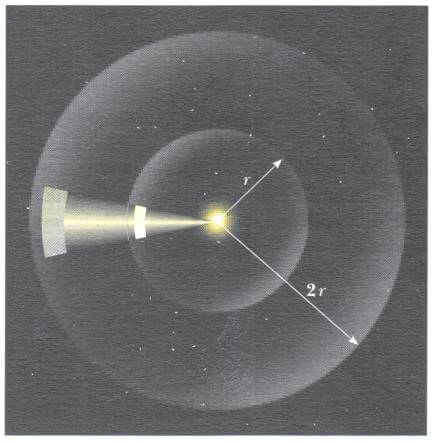
Diğer bir önemli gerçek de şudur: Sonlu büyüklükte ve küresel simetrik olarak dağılmış bir kütlenin küre dışındaki bir parçacığa uyguladığı çekim kuvveti, kürenin tüm kütlesi küre merkezinde toplandığı zaman uygulanacak olanla aynıdır. Örneğin, Dünya (yer/arz küresi) yüzeyine yakın bulunan m kütleli bir parçacığa Dünyanın uyguladığı kuvvet aşağıdaki şekilde verilir.
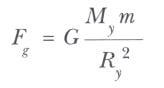
Burada My dünyanın (yerin) kütlesi ve Ry Dünya’nın yarıçapıdır. Bu kuvvet Dünya’nın merkezine doğru yönelmiştir.
Kütle Çekim Sabitinin Ölçülmesi
Kütle çekim sabiti, G, 1798 de Henry Cavendish (1731-1810) tarafından önemli bir deneyle ölçüldü. Cavendish aleti, her biri m kütleli iki küçük küreden oluşur. Küreler yatay, hafif bir çubuğun uçlarına tutturulmuştur ve çubuk, ince bir fiberle veya ince bir metal telle aşağıdaki gibi asılmış durumdadır. Her biri M kütleli iki büyük küre, daha sonra küçük kürelerin yakınma yerleştirildiğinde küçük kürelerle, büyük küreler arasındaki çekici kuvvet çubuğun dönmesine ve tel askının yeni bir denge konumuna kadar burulmasına neden olur. Asılı çubuğun döndüğü açı, düşey askıya yerleştirilmiş olan bir aynadan yansıtılan bir ışık demetinin sapmasıyla ölçülür. Saptırılan ışık demeti, hareketi daha iyi görmenin etkin bir tekniğidir. Deney, farklı uzaklıklardaki değişik kütlelerle dikkatli olarak tekrarlanır. G için birer değer elde edilmesinin yanı sıra, sonuçlar, kuvvetin çekici, mM ile orantılı ve r uzaklığının karesiyle ters orantılı olduğunu da gösterir.
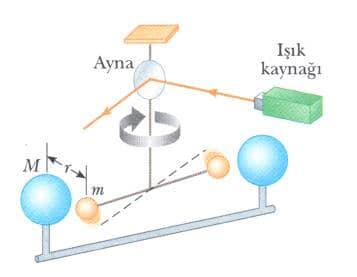
G ’yi ölçmeye yarayan Cavendish düzeneğinin şematik gösterimi, m kütleli daha küçük küreler, M kütleli daha büyük kütlelere doğru çekilirler ve iki küçük küre arasındaki çubuk küçük bir açı ile döner. Dönen düzenek üzerindeki bir aynadan yansıtılan ışık demeti, dönme açısını ölçer. Kesikli çizgi çubuğun ilk konumunu temsil eder.
Serbest Düşme İvmesi ve Kütle Çekim Kuvveti
Dünya (yer) yüzeyine yakın bir yerden serbestçe düşen m kütleli bir cismin üzerine etki eden kuvvet, hemen bir üstteki formülde verildiği için, mg’yi bu ifadeye eşitleyerek aşağıdaki ifadeleri elde ederiz.
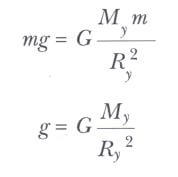
Şimdi dünyanın yüzeyinden h uzaklığı kadar yukarıda veya r= Ry + h olmak üzere, dünyanın merkezinden itibaren r uzaklığında bulunan m kütleli bir cisim alalım. Bu kütle üzerine etkiyen çekim kuvvetinin büyüklüğü ise aşağıdaki gibidir.
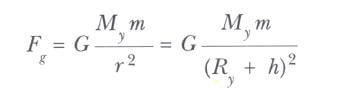
Serbest düşme ivmesinin h yüksekliğindeki değeri g’ olmak üzere, bu yükseklikte cismin üzerine etki eden kütle-çekim kuvveti de Fg= mg’ ile verilir. Bu F ifadesi son eşitlikte yerine konulursa g’:
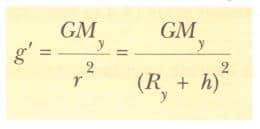
O halde, g’ yükseklik arttıkça azaldığı ortaya çıkar. Cismin gerçek ağırlığı mg’ olduğundan, r → ∞ için ağırlık sıfıra yaklaşır.

