Topoloji: Lastik Geometri, matematiğin birçok alanının olduğunu hepimiz çok iyi biliyoruz. Aslında bu dallar matematik ile uğraşmayan bir kişi için hiçbir anlam ifade etmeyebilir. Lakin öyle bir alan vardır tüm dalların uğraşı haline gelmiştir. Şimdi elinize bir üçgen alın. Bu üçgeni bir kareye ya da çembere çevirmeye çalışın yapabilir misiniz? Galiba cevabınız ne evet ne de hayır olacaktır. Çünkü malzemenin neden olduğunu söylemedik. Peki bir oyun hamurunu alsanız tüm geometrik şekilleri yapabilir misiniz? Şimdi cevabınız evet! İşte bu alan Topoloji biliminin kendisidir.
Topoloji Yunanca “Topos” kelimesinden türemiştir. Bu kelime yüzey, yer ve uzay anlamlarında kullanılmaktadır. Fakat Topoloji bilimi o dönemden bu yana hiç gelişme gösterememiştir. Lakin 19 yy. gelindiği zaman artık matematikçiler topolojinin uzayı anlamızın bir ön koşulu olduğunu vurgulayan makaleler yazması bu bilimin uğraş haline gelmesine olanak kılmıştır. Ama bu alan topoloji olarak değil de Latince analysis situs (konumun analizi) olarak kullanılmaya başlanmıştı. Sonraları ise bazı koşulları sağlayan küme aileleri olarak kullanılmaya başlandı. Aşağıda vermeye çalışacağımız matematiksel bağlantılar geometri yapmanın bir destekleyicisidir yani geometriyi (lisede öğrendiklerimiz değil) anlamanın bir koşulu topoloji bilmektir.
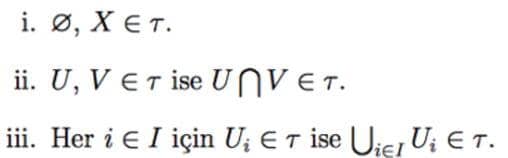τ, X üzerinde bir topoloji ise (X,τ) ikilisine topolojik uzay denir. Yukarıda ne demek istediğimiz anlıyorsunuz değil mi? Boş Kümeden farklı olması, keşimleri ve seçtiğimiz bir eleman için toplamlarının içinde olması gerekmektedir. (X,τ) topolojik uzayına, kısaca topolojik uzay X’de diyebiliriz. Yani, “topolojik uzay X” ya da ”X topolojik uzayı” dediğimizde, X kümesinin belirli bir topoloji ile donatıldığını varsayıyoruz. Bu durumda X, bir küme olmasının yanında (X,τ) ikilisini de temsil etmektedir.
İki küme alalım. Bu iki küme arasında bir topolojik bağlantı tanımlayalım. Şayet bu topolojik bağlantı homeomorfizma denen eş yapılılık kurallarına uygunsa bu iki küme topolojik olarak denktir. Bu tanımlanan eş yapılılık sayesinde bir nesneyi yırtmadan, koparmadan ya da deforme etmeden başka bir nesneye çevirme olanağı tanır.
Hadi şimdi şu yukarıda sözünü ettiğimiz “homeomorfizma” denilen kavramın ne olduğuna bakalım. Aslında bu kelime matematiksel olarak açıklansa da okurun çok net anlaması için örnekler vereceğiz. Elinize bir simit alın. Evet sabahları yediğimiz simit… O simiti alıp bir kahve fincanına dönüştürebilir misiniz? Aynen şöyle,
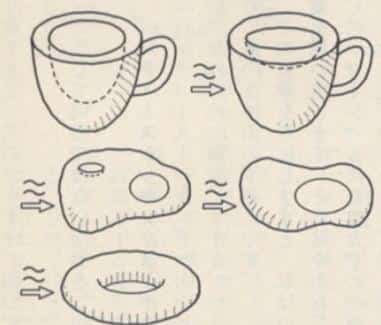Gördünüz mü? Bu çok heyecanlı gerçekten. Şimdi siz de düşünebilirsiniz? Çay bardağını bir çay tabağına dönüştürebilir misiniz? Ödev falan değil sadece düşünün ve çizmeyi deneyin. Bundan sonra yapmanız gereken şey ise üç boyutlu gibi görünen fakat hiç de öyle olmayan topolojik nesnelerimizden “Klein Şişesi” ve “Möbius Şeridi” başlıklı yazılarla devam etmeniz.