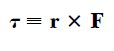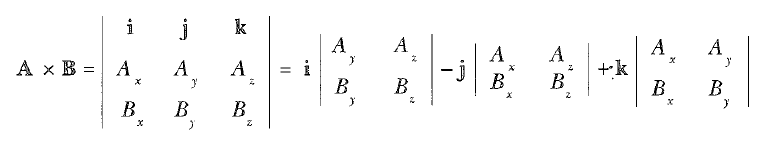Merhaba arkadaşlar bu yazımızda sizlere vektörel çarpım konu anlatımı ve tork nedir konularını anlatacağız. Şekil 1’deki г vektörünün ucunda bulunan katı cisim üzerine etki eden F kuvvetini ele alalım. O başlangıç noktasının bir eylemsizlik referans sisteminde olduğu, bunun sonucu olarak da Newton’un ikinci hareket yasasının geçerli olduğunu kabul edelim. O başlangıç noktasına göre F kuvveti tarafından meydana getirilen dönme momentinin (tork) büyüklüğü, burada gösterildiği gibi tanım olarak, rFsinф ‘уе eşittir. Burada ф; r ve F vektörleri arasındaki açıdır. F, kuvveti tarafından etrafında dönme meydana getirilen eksen, r ve F vektörleri tarafından oluşturulan düzleme diktir. F kuvveti Şekil 1’de olduğu gibi xу – düzlemi içinde uzanırsa, o zaman, т dönme momenti, z – eksenine paralel bir vektörle temsil edilir. Şekil 1 ‘deki kuvvet, z – ekseni doğrultusunda yukarıdan aşağıya doğru bakıldığında, cismi saatin dönüş yönünün tersine döndürmeye çalışan bir tork oluşturur. т, z – ekseni doğrultusunda ve artan z yönündedir. Şekil 1 ’deki F ’nin yönünü ters çevirirsek, o zaman τ, eksi z yönünde yönelir.
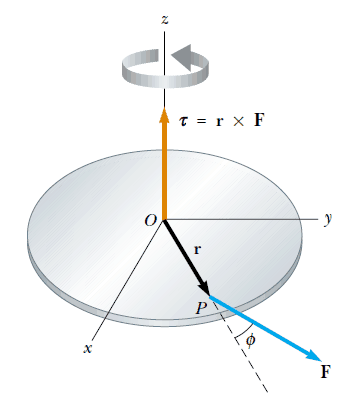
т torku, r ve F gibi iki vektörle ilgili bir niceliktir ve doğrultusu r ve F ’nin oluşturduğu düzleme diktir. Vektörel çarpım denilen matematiksel işlemi kullanarak; т, r ve F arasındaki matematiksel ilişki aşağıdaki gibi tanımlanır:
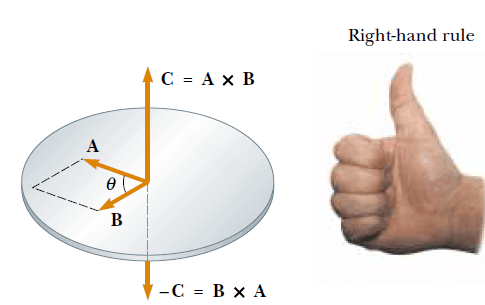
Şimdi, vektörel çarpımın genel bir tanımım veriyoruz. A ve В gibi herhangi iki vektör verildiğinde, А х В vektörel çarpımı, üçüncü bir C vektörü olarak tanımlanır. Bu C vektörünün büyüklüğü, ABsinф ya eşittir, ф ise A ve В vektörleri arasındaki açıdır. Yani, C vektörü
C = A x В (eşitlik 1)
eşitliğiyle verilirse, büyüklüğü
C= AB sinф (eşitlik 2)
olur. Şekil 2’de görüldüğü gibi, ABsinф niceliği, A ve В vektörleri tarafından oluşturulan paralelkenarın alanına eşittir. C’nin doğrultusu, A ve В vektörleri tarafından oluşturulan düzleme diktir ve bu doğrultuyu tayin etmenin en iyi yolu Şekil 2’de gösterilen sağ el kuralını kullanmaktır. Buna göre önce sağ elin dört parmağı A ’yı gösterecek şekilde tutulur. Sonra bu parmaklar B ’ye doğru ф açısı kadar bükülür. Bu durumda yana açılan baş parmak А х В = C yönündedir. Gösterimin şeklinden dolayı, А x B, “A vektörel çarpım B” şeklinde okunur.
Vektörel Çarpım Konu Anlatımından Çıkan Bazı Özellikler
- Skaler çarpımın aksine, iki vektörün vektörel çarpımındaki sıra önemlidir, yani
A x В = -B x A (eşitlik 3)
dır. Bu yüzden, vektörel çarpımdaki vektörlerin sırasını değiştirirseniz, çarpımın işaretini de değiştirmelisiniz. Bu ilişkiyi, sağ-el kuralını kullanarak kolayca gerçekleyebilirsiniz.
- A vektörü B’ye paralelse (ф=0° veya 180°), А х В = 0 olur. Bunun sonucu olarak da A x A = 0 olduğu görülür.
- A vektörü В vektörüne dikse, | A x B | = AB olur.
- Yine vektörel çarpımın, dağılım kuralına uyduğuna dikkat etmek önemlidir, yani:
А х (B + C) = A x B + A x C (eşitlik 4)
- Son olarak, vektörel çarpımın t gibi herhangi bir değişkene göre türevi
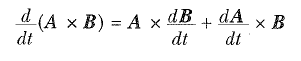şeklinde ifade edilir. Bu işlem yapılırken A ve В vektörlerinin vektörel çarpımdaki sırasını korumak gerekmektedir (3 Eşitliğine bakınız). 2 ve 3 Eşitlikleri ile vektörel çarpımın tanımını kullanarak, birbirine dik i, j ve k birim vektörlerinin vektörel çarpımlarının aşağıdaki eşitlikleri sağladığını gösterebilirsiniz.
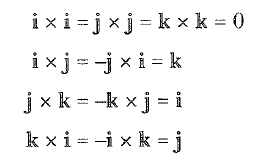Vektörel çarpımda işaretler değiştirilebilir. Örneğin, А х (-B) = -А х В ve i x (-j) = -i x j dir.
A ve В gibi herhangi iki vektörün vektörel çarpımı, aşağıda gösterildiği gibi, determinantla da ifade edilebilir:
Bu determinantların açılımı
olur. Bu yazımızda sizlere vektörel çarpım konu anlatımı ve tork nedir konularını anlattık. Diğer yazımızda görüşmek üzere.