Bu yazımızda 3B Oyun motorlarının yapısını ve matematiğini detaylı bir şekilde anlamaya çalışacağız. Matrislerin nasıl oluştuğunu, neden gibi soruların detayına inmeye çalışacağız. Öncelikle belirtelim bu makaleyi anlamak için en az lise seviyesinde matematik biliyor olmanız gerekmektedir. Genel olarak vektör matematiği ve matrisleri bildiğinizi varsayıyorum.
İlk olarak vektör uzayı ve transformasyon arasındaki ilişkiler hakkında konuşacağız. Sonra bir transformasyonun nasıl matris formunda ifade edilebileceğini göstermeye çalışacağız. Ardından transformasyonun tipik dizilişlerini göstereceğiz ve bir modelden nasıl uygulayacağınızı World uzayında anlatacağız sonra kamera ve daha sonra ise projection’da göstereceğiz.
Vektör Uzayı: Model uzayı ve World Uzayı Nedir?
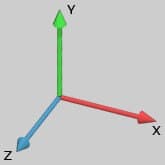
Bir vektör uzayı, lineer olan bağımsız vektörlerin verilen sayısına göre tanımlanan matematiksel bir yapıdır. Ayrıca Vektör Tabanı olarak da isimlendirebiliriz. Resim 1 için örneğin 3 taban vektörü bulunmaktadır: Lineer olan bağımsız vektörün sayısı, vektör uzayının boyutunu tanımlar. Bu nedenle bir 3B uzay 3 taban vektörüne sahip iken 2B uzay 2 taban vektörüne sahip olur. Bu taban vektörleri uzayda tüm diğer vektörleri elde etmek için ölçeklenebilir ve birbirine eklenebilir. Vektör uzayı aslında çok geniş bir konudur ve bizim amacımız tüm bu başlıkları açıklamak değildir. Bizim hedefimiz gerçek bir özel vektör uzayındaki modelimizi, Model uzayı ismi altında incelemek ve kabul edilmiş 3B koordinat sistemi ile temsil etmektir.
Bilgisayar grafiği, bir 3B modeli oluşturduğunda tüm köşe ve yüzeyleri göreceli olarak 3B koordinat sistemine göre haritalandıran bir Model uzayı tanımlaması yapar. Tüm köşeler Model uzayın orijinine göre yapılmıştır. Bu yüzden eğer biz model uzayda (1,1,1) koordinatında bir noktaya sahipsek, nerede olduğumuzu tam olarak biliriz. (Resim 2)
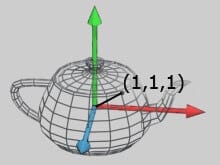
Oyunlardaki her model kendi Model uzayında gerçek-hareketli ve eğer isterseniz onları herhangi bir mekânsal ilişki içerisine sokabilirsiniz. (Çaydanlığı masa üstüne koymak gibi)
Bunları yapmak için ortak bir uzaya (genellikle World uzayı olarak isimlendirilir) onları dönüştürmeniz gereklidir.
Tekrardan vurgulamamız gerekirse bir vektörün, sadece koordinat sistemi içerisinde anlamlı olacağını bilmeniz önemlidir; Biz uzay belirtemiyorsak herhangi bir noktayı tanımlayamayız. Modeller oyun motoru araçlarına dışa aktarıldıktan (export) sonra tüm köşeler Model uzayında tanımlanmıştır. Şimdi oyun dünyasında bir objeyi içeri almak (import) istersek, onu istenilen konuma taşımak ve/veya döndürmeye ihtiyacımız olacaktır. Bunu da nesnenin içerindeki World uzayına yerleştireceğiz. Taşıma, döndürme ya da ölçeklendirmeyi (scaling) bir nesnenin transformasyonu olarak isimlendiriyoruz. Tüm nesneler ortak bir uzay (World Uzay) içerisinde dönüştürülmektedir. Onların köşeleri kendi World uzayına bağlı olacaktır.
Dönüşüm Kavramı- Transformation
Herhangi bir değişiklik için, vektör uzayındaki dönüşümü basitçe başka bir uzaydan görebiliriz. Vektör dönüşümlerinin en zor kısmı bileşenleridir. Bu yüzden her birini açık ve anlaşılır yapmaya çalışacağız.
Bir 3B vektör uzayında 3 ortogonal eksen olduğunu hayal edeceğiz (Resim 1’deki gibi). Daima “Aktif” bir uzaya sahip olmamız gerekiyor. Böylece bu uzayı her şeyin referansı gibi kullanabiliriz (Ya da hem geometri hem de diğer uzaylar için). Eğer her birisi kendi Model uzayında olmak koşuluyla 2 modelimiz varsa, onları ortak bir “aktif” uzayda tanımlayana kadar her ikisini çizemeyiz.
Şimdi aktif bir uzay kavramı ile başlayalım ve bu uzaya A diyelim; bu da bir çaydanlık içeriyor olsun. Şimdi biz A uzayı içerisinde her şeyi yeni bir konum içerisine taşıyan bir dönüşüm uygulamak istiyoruz diyelim. Ancak eğer taşırsak bizim A uzayını, sonradan dönüştürülmüş A uzayını temsil edecek yeni bir aktif uzay tanımlamamız gerekecek. İşte bu yeni aktif uzayımıza B uzayı olarak isim veriyoruz (Resim 3). Dönüşümden önce, A uzayındaki herhangi bir nokta tanımlıdır. A uzayının orijini başlangıç konumuna göredir (Resim 3 en soldaki). Dönüşüm uygulandıktan sonra tüm noktalar şimdi yeni aktif uzaydaki durumuna bağlıdır: B Uzayı (sağdaki). A uzayındaki herhangi bir işlemde B uzayında yeniden tanımlanır ve bu bir dönüşüm olur. Nasıl olduğuna dikkat edin, Dönüşümden sonra a uzayı B uzayı içerisinde kayboluyor ya da daha kesin olarak onu B uzayında yeniden haritalandırıyor. Böylece herhangi diğer dönüşümleri uygulamamız için bizim başka yolumuz olmayacaktır. (Dönüşümleri geri almadıkça ve A uzayını “aktif” uzay yapmadıkça tekrar)
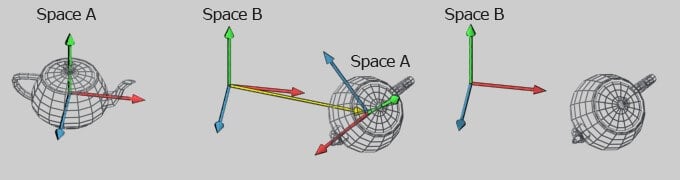
Bunu görmenin diğer yolu, tüm bunları bir uzayda taban vektörleri ile hareket ettiğini hayal edin ve A uzayını B uzayı üstünde mükemmel bir şekilde çakıştırılmış olduğunu düşünün. Dönüşümü yaptığımız zaman bizim A uzayı B uzayından ayrılıyor ve A uzayındaki tüm şeyler onun ile hareketleniyor. Tüm köşeler taşındıktan sonra bizim B uzayımızdaki konumlara göre tanımlı oluyor ve dönüşümü tamamlamış oluyoruz.
Bu durumda A uzayındaki işlemleri tekrar tersine dönüşüm yapmamız (Inverse Transformation) ile B uzayını elde etmemiz de mümkündür. Böylece B uzayı yeniden haritalanabiliyor olacak A uzayı içerisinde yeniden (ve bu noktaları biz “kaybederiz” B uzayında). Eğer hem dönüşümünü hem de onların tersini (inverse) biliyorsak daima yeniden 2 uzayı, birini diğerinden yeniden haritalandırabiliriz.
Vektör uzayındaki dönüşümleri ölçeklendirme (scale), öteleme (translation), döndürme (rotation) için kullanırız. Burada önemli bir nokta, tüm dönüşümler daima orijine göre tanımlıdır. Eğer 900 sol ve sonra öteleme yaparsak farklı bir şey eğer ilk öteleme sonra 900 döndürme yaparsak farklı şeyler yapmış oluruz. (Resim 4, tüm uzayı birbirinden Aktif olduğunu ihmal ediyoruz)
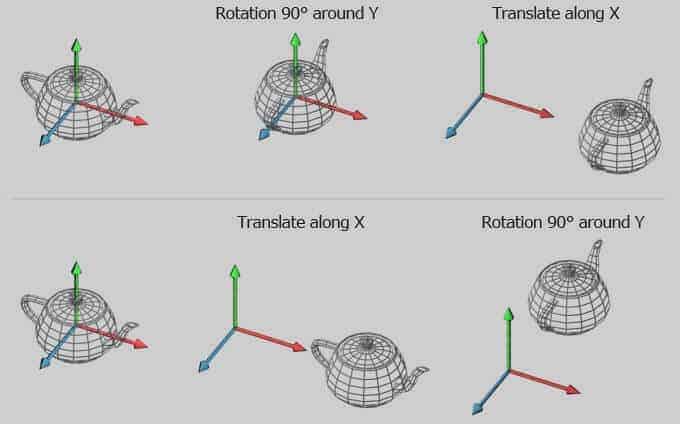
Resim 4 ayrıca bir dönüşümün tersini anlamamızda da bize yardımcı olabilir. Eğer resim 4 sol üstü ele alırsak 900 ‘lik dönüş, sol tarafa transformasyonu alınarak (yeniden taşınmasıyla) yani onun tersi ile de elde edilebilir.
Dönüşüm Matrisi – Transformation Matrix
Şimdi biz biliyoruz ki bir dönüşüm bir uzaydan diğerine olan değişimdir ve bunu matematiksel olarak yapabiliriz. Eğer 3B uzayı olan bir dönüşümü diğerine temsil etmek istersek 4×4’lük bir matrise ihtiyacımız olacak. OpenGL’deki gibi, bir sütun vektör notasyonu üzerinden bunu anlatmaya çalışacağız. Eğer satır vektörleri içerisindeyseniz sadece devrik (transpose) matrise ve çarpılabilir vektörlere ihtiyacınız olacaktır. Dönüşümleri uygulamak amacıyla tüm vektörleri çarpılabilir yapmamız gereklidir. Eğer A uzayındaki vektörler ve dönüşümler A uzayının yeni konumu B uzayına göre tanımlanabiliyorsa, çarpmadan sonra tüm vektörler B uzayında sonradan tanımlanabilir olacaktır.
Şimdi Matris formunda nasıl genel bir dönüşüm temsil ediliyor onu inceleyelim:
- Transform_XAxis yeni uzaydaki X ekseninin oryantasyonu veya yönelimidir.
- Transform_YAxis yeni uzaydaki Y eksenin yönelimidir.
- Transform_ZAxis yeni uzaydaki Z eksenin yönelimi veya yönüdür.
- Ve Translation ise yeni uzayın aktif uzaya göre olacağı konumu açıklar.
Bazen basit dönüşümler yapmak isteriz, dönme veya taşıma gibi; bu gibi durumlarda aşağıdaki gibi bazı basit formları kullanabiliriz.
Öteleme Matrisi – Translation Matrix
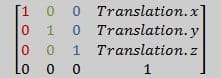Öteleme bir 3B vektörü uzayımızda taşımak istediğimiz bir konumu temsil etmektedir. Bir öteleme matrisi, aktif uzayda tam olarak döndürülmüş tüm eksenleri bırakır.
Ölçekleme Matrisi – Scale Matrix
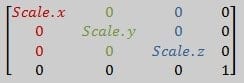Her bir eksen boyunca ölçeği tanımlayan bir 3D vektördür. İlk sütunu okursanız yeni X eksenin nasıl olduğunu görebilirsiniz. Hala aynı yöne bakacak şekilde duruyor ancak Scale.x tarafından ölçeklendirilmiş şekildedir. Bunun yanı sıra tim diğer eksenlerde de aynı şeyler olur. Ayrıca translation sütunlarının ( en sağdaki siyah olan sütün ) bu sefer 0 olduğuna dikkat edin, bunun anlamı öteleme yapılmadığını gösteriyor.
X Ekseni Etrafındaki Dönme Matrisi – Rotation Matrix
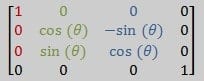Teta, bizim dönüş yapmak için kullanmak istediğiniz. X ekseni etrafında dönüş yapıyor olacağımızdan ilk sütünün asla değişmeyeceğini unutmayın! Ayrıca tetanın 900 ‘lik değişikliğinin nasıl Y eksenini Z ekseni içerinde ve Z eksenini de –Y ekseni içerisinde yeniden haritalandırdığına dikkat edin.
Y Ekseni Etrafındaki Dönme Matrisi Z Ekseni Etrafındaki Dönme Matrisi
Z ve Y ekseni için Dönme Matrisleri X ekseni etrafındaki dönme matrisiyle aynı davranışlara sahiptir.
Biz burada sadece en çok kullanılan bazı matrisleri anlattık. Birbiri ardına matrisleri çarpım şekline getirerek onları zincir dönüşümü şeklinde yapabilirsiniz. Sonuç tam bir dönüşümü şifreleyen tek bir matris olacaktır. Dönüşüm bölümünde gördüğümüz gibi transformasyonları uygulamalı olarak kullanabilmemiz çok önemlidir. Matematikteki çarpımda yer değişim özelliği burada biraz farklıdır çünkü Öteleme x Dönme ile Dönme x Öteleme birbirinden farklıdır.
Sütun vektörleri kullandığımızdan dolayı bir zincir dönüşümünü sağdan sola doğru okuyacağız. Bu yüzden eğer istersek 900 dönüşü Y ekseni etrafında sola doğru ve sonra 10 birimlik ötelemeyi Z eksenine doğru bir zincir şeklinde sıralayabiliriz.
[Öteleme 10 birim Z Boyunca]x[Dönme 90° Y Etrafında]= [Karma Dönüşüm]
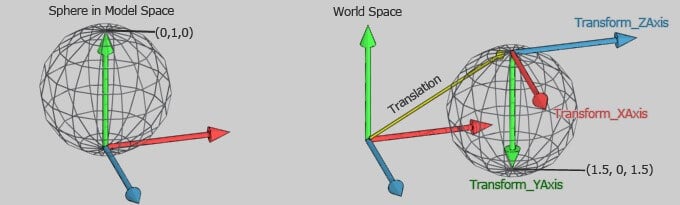
Şimdi bazı sayılar vererek olayın nasıl çalıştığına bakalım. Resim 5 deki küreyi ele alalım. Bunun dönüşümünü yapmak istiyoruz. Basitlik açısından kürenin üst noktasından dönüşümü uygulamaya başlayacağız. Model uzayında buranın konumu (0,1,0) şeklidedir. World uzayında nerede olacağını hesaplayacağız. Her şeyden önce ilk dönüşüm matrisini bulacağız. World uzayında kürenin nerede konumlandırılmış olduğunu söylemek istiyoruz. 900 saat yönü için Y ekseni etrafında döndürülecek sonra X ekseni etrafında 1800 döndürülecek ve artından (1.5, 1, 1.5) konumuna ötelenecektir. Yani bunun anlamı dönüşüm matrisi şu şekilde olması gerekiyor:
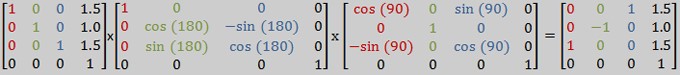
Sonuç matrisini nasıl mükemmel Genel Dönüşüm formülü şeklinde bulduğumuzu fark edin. World uzayında X ekseni (kürenin) şimdi uzayın Z ekseni gibi bir doğrultuda yönlendiğini yani (0,0,1) olduğuna dikkat edin (Kırmızı X, Yeşil Y, Mavi Z eksenidir). Y ekseni şimdi ters çevrilmiş dolayısıyla (0,-1,0) şeklindedir. Z eksenide X ekseni doğrultusuna (1,0,0) yönlenmiş şekildedir. Sonuç olarak Dönüşüm vektörü (1.5, 1, 1.5) olmaktadır.
Model uzayından World uzayı içerisine kürenin herhangi bir uç noktasını çarpım şeklinde sonucunu gösterebiliriz. Bizim uç noktamız (0,1,0) denersek yandaki şekilde ifade edilir. 4×4 matris kullandığımızı ve homojen koordinatlara ihtiyacımız olduğuna dikkat edin. Bu nedenle son bileşeni 1 olan 4 boyutlu vektöre gereksinimiz vardır.
Konu karışık ve anlamsız gelebilir bu yüzden Kamera ve Projection ile alakalı bölümleri ilgi oranına göre yazacağım.