Admitans Nedir

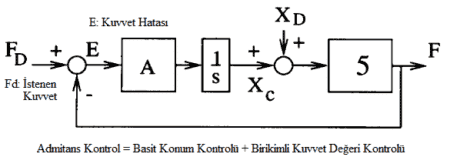
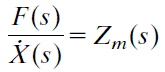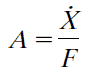Admitans (admittance) kontrolü. Mekanik admitans aşağıdaki şekilde tanımlanır:

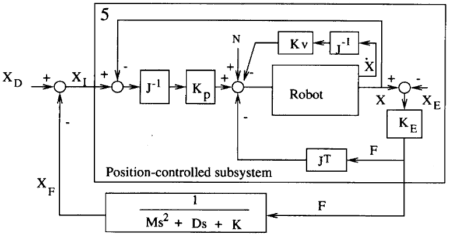
Admitans (2) empedansın (1) tersi olarak ifade edilir. Aşağıdaki şekilde kutu 5 içinde kalan kısım ortak kontrol yapısını göstermektedir. Admitans matrisi A, kuvvet hata vektörünü E (E=F_d-F) uç efektör hızındaki bozulmayla ilişkilendirmektedir. Bilinen bir çevresel sertlik (stiffness) için, az veya sıfır hata ile düşük aşma ve hızlı yükselme süresinde istenen bir kuvvet tepkisini (desired force) elde etmek için bir A admitansı yapılabilir. Komut yörüngesi Xc aşağıdaki gibi tanımlanır:

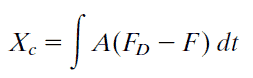
Empedans kontrolü ile karşılaştırırsak, admitans kontrolü istenilen kuvvete (desired force) daha fazla odaklanır.

Hibrid Kontrol

Hibrid Konum/Kuvvet Kontrolü

Hibrid konum/kuvvet kontrolü, kuvvet ve tork bilgisini konum verisiyle birleştirir. Mason kavramı temel alınarak yer değiştirme ve kuvvet konusunda iki tamamlayıcı ortogonal (dik açılı) çalışma alanını tanımlar. Hibrid konum/kuvvette, konum kontrolü ve kuvvet kontrolü ayrı olarak dikkate alınabilir. Hibrid kontrol yönteminin verimliliği ilk olarak bir Scheinman kolunda doğrulanmıştır.

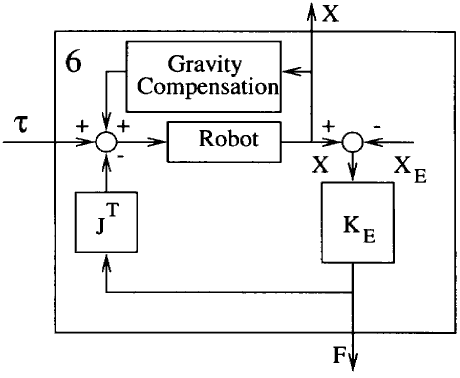
Aşağıdaki şekil hibrid konum/kuvvet kontrol şemasını göstermektedir. S=diag(s_j) (j=1…n) uygunluk (seleksiyon, ayırma) matrisi – compliance selection matrix – olarak ifade edilir ve n serbestlik derecesidir.

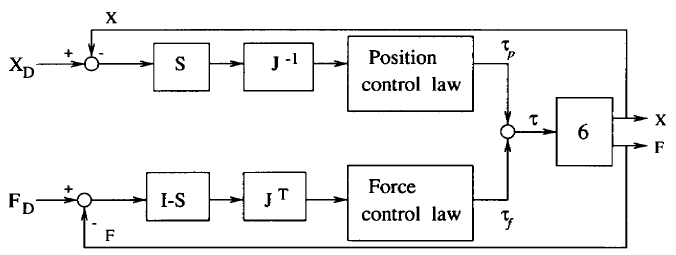
Matris S, kuvvet veya pozisyonun kontrol edileceği alt uzayları belirler ve s_j, 1 veya 0 olarak seçilir. s_j=0 olduğunda, j’inci serbestlik derecesi (DOF) kuvvetle kontrol edilmelidir, aksi halde konum kontrollü olmalıdır. Komut torku;

τ = τ_p + τ_f olup,

burada τ_p ve τ_f sırasıyla konum ve kuvvet alt uzayların da hareket eden komut torklarıdır. Bu şekilde, konum kontrolü ve kuvvet kontrolü ayrıştırılır. Her biri için kontrol yasaları bağımsız olarak tasarlanabilir, böylece istenen konum ve kuvvet izleri takibi için farklı kontrol performans gereksinimleri eş zamanlı olarak gerçekleştirilir.

Normal olarak, yukarıdaki şekilde pozisyon kontrol yasası bir PD (Hatırlayın PID kontrol) kontrolcüden oluşur ve kuvvet kontrol yasası da bir PI kontrolcüden oluşur. Bunun amacı, konum kontrolü için daha hızlı bir cevabın alınmak istenmesi ve kuvvet kontrolü için de daha küçük bir hatanın olması istendiğindendir.

Hibrid Empedans Kontrolü

Hibrid empedans kontrolü, empedans kontrolü ve hibrid konum/kuvvet kontrolünü tek bir stratejide birleştiren Anderson ve Spong tarafından önerilmiştir. Bir tasarımcının robotik sistemini istenen empedansını seçmede daha fazla esneklik sağlamasına olanak tanır. Kuvvet kontrollü ve pozisyon kontrollü alt uzaylarda empedans ayrımı yapılabilir. Bu nedenle, hız (veya konum) gereksinimlerinin muhafaza edilmesine ek olarak, kontrollü bir kuvvet yörüngesi takip edilebilir. Aşağıdaki şekilde, hibrid empedans kontrol bloğu diyagramını göstermektedir.

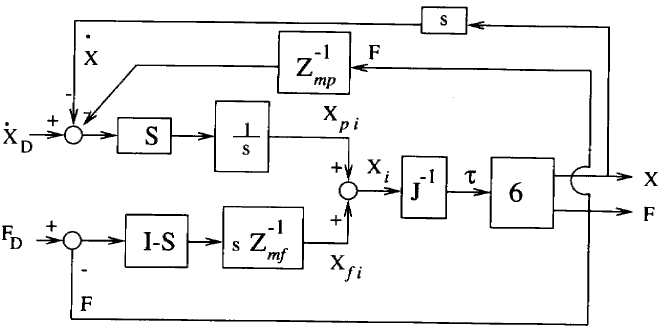
Bu şekilde, Z_mp ve Z_mf kullanıcı tarafından seçilen istenen empedans (desired impedance) terimleridir. Eğer diyagonal (köşegen) matris olarak seçilirlerse, elemanları empedansın her bir serbestlik derecesini gösterir. S, hibrid konum/kuvvet kontrolündeki ile aynı olan uyum seçim matrisidir (compliance selection matrix). Modifiye edilen istenen yörünge X_i aşağıdaki gibidir:

X_i = X_pi + X_fi

X_pi ve X_fi sırasıyla, konum ve kuvvet alt uzayında ifade edilen modifiye pozisyon ve kuvvet yörüngeleridir.

Kararlılık Sorunları

Hibrid konum/kuvvet kararlılık sorunları için referansları inceleyebilirsiniz [1][2][3-5]. Hibrid konum/kuvvet kontrolü için genelleştirilmiş bir mimari verilmiştir [6]. Lyapunov’un doğrudan yöntemini kullanan lineer olmayan hibrid kontrol stabilitesi analiz edilmiştir ve hibrid kontrol algoritması için temel kararlılık koşulları da gösterilmiştir. [7]

Kaynak
An overview of robot force control – Ganwen Zeng and Ahmad Hemami, depertment of electrical engineering and computer science. Robotica (1997) volume 15, pp 473-482.

Referanslar

[1] C. H. An and J. M. Hollerbach, ‘‘The Role of Dynamic Models in Cartesian Force Control of Manipulators’’ Int. J. of Robotics Res. 8 (4), 51 – 71 (1989).
[2] E. De´ goulange and P. Dauchez, ‘‘External Force Control of an Industrial PUMA 560 Robot’’ J. of Robotics Sys. 11 (6), 523 – 540 (1994).
[3] W. D. Fisher and S. Mujtaba, ‘‘Hybrid Position/Force Control: A correct formulation’’ Int. J. of Robotics Res. 11 (4) , 299 – 311 (1992).
[4] S. H. Murphy and J. T. Wen, ‘‘Stability Analysis of Position and Force Control for Robotic Arms’’ IEEE Trans. on Automatic Contr. 36 (3), 365 – 371 (1991).
[5] T. Yabuta, T. Kamada, T. Tusjimura and H. Saksta, ‘‘Force Control of Servomechanism Using Adaptive Control’’ IEEE Int. J. of Robotics and Automat. 4 (2) , 223 – 228 (1988).
[6] T. Yabuta, ‘‘Nonlinear Basic Stability Concept of the Hybrid Position/Force Control Scheme for Robot Manipulators’’ IEEE Trans. on Robotics and Automat. 8 (5), 663 – 670 (1992).
[7] H. Seraji, ‘‘Adaptive Admittance Control: An Approach to Explicit Force Control in Compliant Motion’’ IEEE Int. Conf. on Robotics and Automation (1994) pp. 2705 – 2712.

An overview of robot force control – Ganwen Zeng and Ahmad Hemami, depertment of electrical engineering and computer science. Robotica (1997) volume 15, pp 473-482.