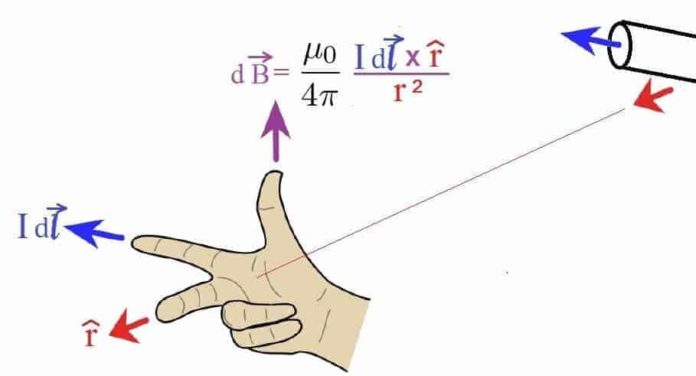
Oersted’in 1819’da akım taşıyan bir iletkenin bir pusula iğnesini saptırdığını keşfinden kısa bir süre sonra, Jean Baptiste Biot (1774-1862) ve Felix Savart (1791-1841) bir elektrik akımının yakınındaki bir mıknatısa uyguladığı kuvvetle ilgili nicel deneyler yaptılar. Biot ve Savart deneysel sonuçlardan yola çıkarak uzayın bir noktasındaki manyetik alanı, bu alanı oluşturan akım cinsinden veren matematiksel bir ifade buldular. İfadede, kararlı bir I akımı taşıyan bir telin bir ds uzunluk elemanın P noktasında oluşturduğu dB manyetik alanı aşağıdaki deneysel gözlemlerine dayanır.
- dB vektörü, hem ds (akım yönündedir) ye ve hem de ds den Pye doğru yönelen r birim vektörüne diktir.
- dB’nin büyüklüğü r ile ters orantılıdır. Burada r, ds nin P ye uzaklığıdır.
- dB’nin büyüklüğü akımla ve ds uzunluk elemanın büyüklüğü, yani ds ile orantılıdır.
- dB’nin büyüklüğü sin θ ile orantılıdır. Burada θ, ds ve r vektörleri arasındaki açıdır.
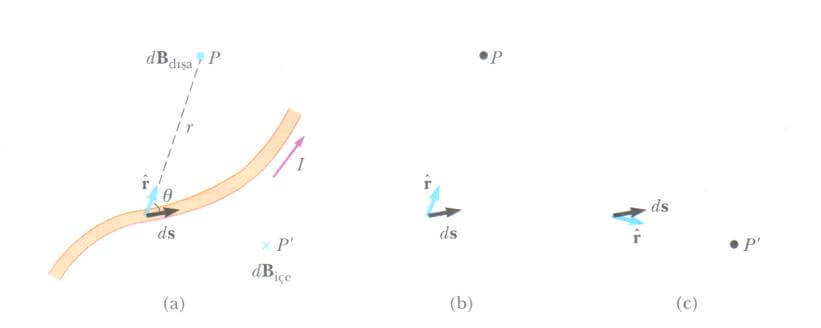
manyetik alanı Biot-Savart yasasıyla verilir. P deki manyetik alanın yönü sayfa düzleminden dışa ve P’ deki ise içe doğrudur, (b) r , P ye doğru baktığında ds x r vektörel çarpımının yönü sayfa düzleminin dışına doğru olur, r , P’ ye yönelirse ds x r sayfa düzleminin içine doğru olur.
Bu gözlemler bu gün, Biot Savart yasası olarak bilinen aşağıdaki matematiksel bağıntıyla özetlenebilir.
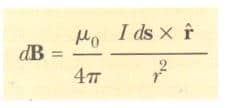
Burada μ0 serbest uzayın geçirgenliği denen bir sabittir.
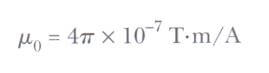
Eşitlik’deki dR alanının, iletkenin yalnız küçük bir ds uzunluk elemanındaki akımın oluşturduğu alan olduğuna dikkat etmek son derece önemlidir. Sonlu büyüklükteki bir akımın, bir noktada oluşturduğu В toplam manyetik alanını bulmak için, akımı oluşturan tüm Ids akım elemanlarından doğan katkıları toplamamız gerekir. Yani, B’yi eşitliğin integralini alarak bulmalıyız.
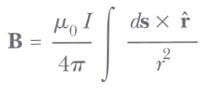
Burada integral akım dağılımının tamamı üzerinden alınır. Bu ifade özel bir dikkatle kullanılmalıdır, çünkü integralin içinde vektörel bir nicelik bulunmaktadır.
Biot-Savart yasası, bir akım taşıyan tel için geliştirilmiş olmasına rağmen, bir televizyon setindeki elektron demeti gibi uzayda akan yüklerden oluşan bir akım için de geçerlidir. Bu durumda ds, yükün aktığı uzayın küçük bir parçasının uzunluk elemanıdır.
Manyetizmanın Biot Savart yasası ile elektrostatiğin Coulomb yasası arasında ilginç benzerlikler vardır. I ds akım elemanı bir manyetik alan oluşturur buna karşılık bir q nokta yükü elektrik alan oluşturur. Ayrıca, nokta yükten kaynaklanan elektrik alanı gibi, manyetik alanın büyüklüğü de akım elemanından uzaklığın karesi ile ters orantılı olarak değişir. Ancak, iki alanın yönleri oldukça farklıdır. Nokta yükün oluşturduğu elektrik alanı yükten çıkan doğrular boyuncadır (radyal). Fakat, bir akım elemanının oluşturduğu manyetik alan, Eşitlikteki vektörel çarpım gereği hem ds akım elemanına ve hem de r birim vektörüne diktir. Bu yüzden, iletken kağıt düzleminde bulunuyorsa, Şekil’de olduğu gibi, dR, P noktasında kağıt düzleminden dışa ve P’ ’de içe doğru yönelmektedir.
Elektrik ve manyetik alanlar arasındaki bir başka farklılık alanın kaynağı ile ilgilidir. Elektrik alanı, yalıtılmış bir elektrik yükü tarafından oluşturulur. Biot-Savart yasası yalıtılmış bir akım elemanının bir noktada oluşturduğu manyetik alanı verir, fakat böyle bir yalıtılmış akım elemanı, bir yalıtılmış yükün bulunabildiği şekilde bulunamaz. Bir akım elemanı, sürekli bir akım dağılımının bir parçası olmak zorundadır. Çünkü yüklerin akması için devremiz tam olmalıdır. Bu nedenle Biot-Savart yasası, bir manyetik alanı hesaplarken yalnız ilk adımdır. Bundan sonra akım dağılımı üzerinden integral almak gerekir.