Diferansiyel Denklemler Nedir

Bir nesne nasıl düşer? Nüfus nasıl artar? Isı bir maddede nasıl yayılır? Salgın hastalıklar nasıl yayılır? Tüm bu soruların cevabı diferansiyel denklemlerde gizlidir! Matematiğin en güçlü araçlarından biri olan diferansiyel denklemler, değişimi ve hareketi anlamamızı sağlar. Gelin, bu büyüleyici matematik dalının dünyasına birlikte adım atalım!

Diferansiyel denklemler, tıpkı evrenin gizli dilini çözmek gibidir. Doğanın karmaşık davranışlarını zarif matematiksel formüllere dönüştürür. Newton’dan Einstein’a, tüm büyük fizikçiler bu dili konuşmuştur!

Diferansiyel Denklem Nedir? Değişim Hızının Formülü

Diferansiyel denklem, bir fonksiyonu ve bu fonksiyonun türevlerini içeren denklemdir. Daha basit bir ifadeyle, bir büyüklüğün nasıl değiştiğini, değişim hızını ve bu değişimi etkileyen faktörleri matematiksel olarak ifade eden denklemlerdir.

Matematikte fonksiyon, bir değişkene bağlı olarak değişen büyüklüktür (örneğin y = f(x)). Türev ise fonksiyonun değişim hızıdır (dy/dx veya f'(x)). Diferansiyel denklem, bu türevi içeren bir denklemdir:

dy/dx = f(x)

Bu basit bir diferansiyel denklemdir. Daha karmaşık olanlar ikinci, üçüncü veya daha yüksek mertebeden türevler içerebilir:

d²y/dx² + 3dy/dx + 2y = 0

Peki bu ne işe yarar? Diyelim ki bir cismin hızını biliyorsunuz (hız, konumun türevi değil mi?). Diferansiyel denklemi çözerek cismin konumunu bulabilirsiniz! Ya da bir popülasyonun büyüme oranını biliyorsanız, gelecekteki nüfusu tahmin edebilirsiniz.

Diferansiyel denklemler, statik durumları değil dinamik süreçleri anlatır. Fotoğraf yerine video gibi – hareketi, değişimi ve zamanı içerir!

Diferansiyel denklemler, en basit biçimiyle, bir x(t) fonksi­yonu, bunun x'(t) türevi ve t değişkeni arasında bir bağıntı olarak tanımlanabi­lir. Bu üç büyüklüğün söz konusu oldu­ğu bir eşitlik olarak ortaya çıkar. Böyle bir denklemi çözmek, en iyi durumda, t’nin her değeri için denklemin doğrulanacağı x(t) fonksiyonunu bulmaktır. Somut bir gösterimde, t zaman olarak alındığında x(t), noktanın izlediği yol ve x'(t) hızıdır ve diferansiyel denklem, konum ve hız arasında her an var olan bağıntıyı belirtir; bu denklemi çözmek, buna uyan bir hareketi betimlemek an­lamına gelir.

Diferansiyel denklemler, birçok fonk­siyonun söz konusu olduğu birçok, ba­ğıntı göz önüne alınarak, daha genel şekilde tanımlanabilir: böyle bir tanım ya­pılması halinde bir diferansiyel sistem or­taya çıkar. Öte yandan, söz konusu fonksiyonun birinci türevinden başka, daha yüksek basamaktan türevleri de söz konusu olabilir.

Diferansiyel denklemlerin genel çö­zümü, matematiğin en zor problemle­rinden biridir. Bu denklemlerin, tipleri­ne göre sınıflandırılması yoluna gidildi, ilk sınıflandırma öğesi, kullanılan türevlerin derecesidir: birinci ve ikinci türev­lerin kullanıldığı bir diferansiyel denk­lem ikinci derecedendir. İkinci sınıflandırma öğesi, cebirsel biçimdir; nitekim, doğrusal, ikilenik vb denklemler vardır.

Bir diferansiyel denklemi çözmek i- çin, denklem, çözümü bilinen, ama bili­nen fonksiyonlar arasında çözümler bu­lunduğundan emin olunmayan bir sını­fa yerleştirilir. Yapılan bu işlem bazen yeni fonksiyonların oluşturulmasına yol açabilir; mesela üslü fonksiyon,

denkleminin çözümü ola­rak tanımlanmıştır. Diğer yandan, çö­zümün biçimi yalnız denklem tipini in­celeyerek anlaşılamaz; nitekim,

denkleminin k’nın değer­lerine göre farklı çözümleri vardır; k ’nın bazı değerleri için, çözüm, dönemsel bir fonksiyondur; armonik salınım üreteç­leri buna iyi bir örnektir.

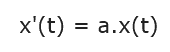
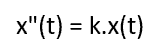
Daima n’inci dereceden bir denklem, birinci dereceden n denklemli bir siste­me eşdeğer hale getirilebilir. Bu du­rumda denklem mekanik modelden esinlenerek bir vektör alanı olarak yorumlanabilir; bu alanın her P noktası fazlar uzayında gelişimini sürdüren soyut bir sistemin bir durumunu temsil eder. Bu noktaya eşlik eden vektör, sistemin ge­lişiminin anî hızını belirtir. Bu hızın sıfıra indiği nokta, tekil nokta adını alır; bu noktanın özel bir rolü var­dır; çünkü tek başına, denklemin çözü­münü verir.

Denklemin çözümüne integral çizgisi denir ve bu soyut P noktasının izlediği yol (yörünge) olarak yorumlanabilir. Bazen, integral çizgiler, yaklaşıklık yöntemleriyle belirlenebilir.

Üslü Fonksiyonun Bulunmasını Sağlayan Bu (x’ = ax) Diferansiyel Denklemler

Bir topluluğun nüfusunu göz önüne alalım. Bireylerin sayısının değişim oranı ve bu oranın zaman içinde değişmediği biliniyorsa, bu sayının ne şekilde değişeceği öngörülebilir. Bu oran küçük olsa bile, pozitif olduğu andan itibaren, nüfus daha hızlı artacaktır. Bu sonuç kuşkusuz, bireylerin başlangıçtaki sayısı sıfır değilse doğrudur. Burada, zaman içinde gelişen ve farklı durumları bir sayıyla belirtilen bir sistemle karşı karşıyayız; herhangi bir anda, sistem sa­yısıyla gösterilebilirse, bu andan hemen önceki ve sonraki durumların p + ap’ye çok yakın sayılarla belirtilmesini sağlayacak bir a sayısı vardır. Başka bir deyişle ap, sistemin p durumundaki değişiminin anî hızıdır. Sistemin yerel değişimi, her p sayısına ap sayısını bağlayan tek gerçek değişkenli ve gerçek değerli fonksiyonla gösterilebilir. Bu fonksiyon, ap değerleri hız vektörleri biçiminde yorum­landığından, vektör alanı diye adlandırılır.

Bu yerel betimle­meden sonra sıfır adı verilen belli bir andaki durumu bilmek ko­şuluyla, sistemin olabildiğince uzun bir zaman aralığındaki gelişimini belirleme problemi ortaya çıkar. Başka bir deyişle, bir t anına, x(0) bilinmek koşuluyla, x'(t) = ax(t) eşitliğini doğrulayacak x(t) sayısını bağlayan bir x fonksiyonu aranır. Bu durumda problemin çözümü x(0) başlangıç koşulu bilin­diğine göre, x = ax diferansiyel denklemi çözülerek elde edilir. Bu denklemin çözümleri olan fonksiyonlar (bunlara, denklemin integralleri adı verilir), sis­temin olası değişimlerini belirtir. Matematiksel yöntemler, x’= ax denkleminin integrallerinin, e^at üslü sayısı ile x(0) başlangıç değerinin çarpımını t ’ye eşlik ettiren x fonksiyonları olduğunu göstermeye imkân verdi. Bir üslü sayı hiçbir zaman sıfır olamayacağına göre, x(t) ancak x(0) = 0 ise sıfır olabilir; yani, bu durumda, fonksiyon sürekli olarak sıfır kalır ve bu da, bir nüfus örneği düşünüldüğünde, tutar­lıdır.

Sıkça Sorulan Sorular (SSS)

1. Diferansiyel denklemleri öğrenmek zor mu?

Dürüst olmak gerekirse, diferansiyel denklemler ilk bakışta göz korkutucu görünebilir ama sistematik yaklaşımla öğrenilebilir. Öncelikle kalkülüs bilgisi (türev, integral) şarttır – diferansiyel denklemler kalkülüsün devamıdır. Temel türleri ve standart çözüm yöntemlerini öğrenince, çoğu problem benzer kalıplara girer. Başlangıçta basit birinci mertebe lineer denklemlerle başlayın, sonra kademeli ilerleyin. Bol pratik yapın – matematik kas hafızası gerektirir! Online kaynaklar (Khan Academy, MIT OpenCourseWare), ders kitapları ve örnekler yardımcı olur. MATLAB, Python gibi araçlar sayısal çözümü kolaylaştırır – her denklemi elle çözmenize gerek yok. Zorlanırsanız, fiziksel anlamını düşünün: “Bu denklem ne anlatıyor?” Soyut matematik yerine gerçek dünya bağlamında düşünmek kavramayı kolaylaştırır. Sabır ve pratikle herkes öğrenebilir!

2. Diferansiyel denklem çözmek için hangi yazılımlar kullanılır?

Modern mühendislik ve bilimde diferansiyel denklemler genellikle yazılımlarla çözülür. Popüler araçlar: MATLAB: En yaygın mühendislik yazılımı, ode45, ode23 gibi hazır fonksiyonlar var. Güçlü, ama ücretli. Python: Ücretsiz ve açık kaynak! SciPy kütüphanesi (solve_ivp, odeint fonksiyonları) mükemmel. NumPy, Matplotlib ile birlikte tam paket. Mathematica: Sembolik ve sayısal çözüm, güçlü görselleştirme. Akademide popüler. Maple: Mathematica’ya benzer, sembolik hesaplama. R: İstatistik ve veri bilimi için, deSolve paketi diferansiyel denklem çözer. Julia: Yeni nesil bilimsel hesaplama dili, DifferentialEquations.jl paketi çok güçlü. COMSOL, ANSYS: Mühendislik simülasyonları için, kısmi diferansiyel denklemler çözer (ısı transferi, akışkanlar, yapısal analiz). Başlangıç için Python önerilir – ücretsiz, öğrenmesi kolay ve iş hayatında çok kullanılır!

3. Diferansiyel denklem bilmeden mühendis olunabilir mi?

Teorik olarak diploma alabilirsiniz ama pratikte gerçek bir mühendis olamazsınız! Diferansiyel denklemler mühendisliğin temel dillerinden biridir. İnşaat mühendisliği (yapı dinamiği, titreşim analizi), makine mühendisliği (ısı transferi, akışkanlar mekaniği), elektrik mühendisliği (devre analizi, kontrol sistemleri), kimya mühendisliği (reaktör tasarımı, proses kontrolü) – her alanda diferansiyel denklem kullanılır. Simülasyon yazılımları (ANSYS, MATLAB) arka planda diferansiyel denklem çözer – siz farkında olmasanız bile! Mühendislik lisans eğitiminde diferansiyel denklemler zorunlu derstir ve çoğu ileri dersin ön koşuludur. Evet, günlük rutin işlerde belki doğrudan çözmezsiniz ama sistemleri anlamak, problemleri modellemek ve yazılım sonuçlarını yorumlamak için gerekir. Sonuç: Başarılı bir mühendis için diferansiyel denklem bilgisi şarttır. İyi haber: İş hayatında genellikle yazılımlar çözer, siz yorumlarsınız!