Bu otel zengin olmak için size göre… Matematiğin teoremleri, ispatları, tanımları bir yana dursun ilginç bir matematiksel düşünceden bahsedelim. David Hilbert 1900’lü yıllarda kendi ismiyle anılan ve sonsuzluk kavramına bir bakış açısı getirmek için ortaya atılmış müthiş bir örnektir.
Bir otel görüyorsunuz ve görevliye bu otelde kalmak için soruyorsunuz fakat odaların hepsinin dolu olduğunu söylüyor. Oteldeki oda sayısı sonsuzdur.
Soru-1: Oteldeki tüm odalarınız dolu ve bir müşteri geldiğinde bu müşteriyi yerleştirebilir misiniz?
Hilbert bu sorunun cevabının çok basit bir şekilde açıklanacağını şöyle vurgulamıştır. 1. odada kalan kişi 2. odaya, 2. odadaki kişi 3. odaya bu şekilde n. odadaki kişi n+1. odaya yerleştirilerek 1. odayı boşaltmış oluruz ve gelen misafir yerleşmiş olur.
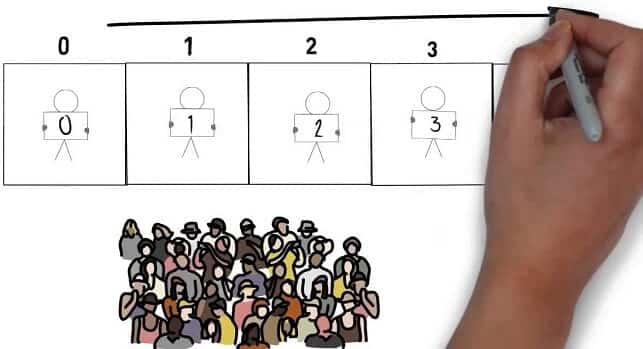Bu soru ve cevap aslında gülünç bir ifade etmiş olabilir siz de fakat bu matematiksel olarak şu anlama geliyor. Sonsuza bir eklenirse ne olur? Cevap yukarıda…
Hilbert bir adım daha ileri giderek soruyu şöyle sormuştur.
Soru-2 : Otelinizin başında bekliyorsunuz ve işler kesat. Odalarınızın tümü boş. Beklenmedik şekilde otelinizin önüne içinde sonsuz tane insan bulunan bir otobüs geliyor ve ardından yine sonsuz sayıda insan olan başka bir otobüs geliyor. Otele nasıl yerleştireceğiz?
Bu soruyu şöyle açıklayacağız daha doğrusu Hilbert tarafından açıklandı. İki otobüste de sonsuz sayıda insan var. Birinci otobüse K otobüsü diğer otobüse L otobüsü diyelim. K otobüsündeki her bir yolcuya k1, k2, k3, gibi isimler verelim. (Kapı açıldığında inen ilk yolcu k1 olarak nitelendireceğiz) Diğer otobüste de aynı biçimde kapı açıldığında birinci yolcuya L1, L2, L3 gibi numaralandıralım. Yerleştirme işlemini şöyle yapacağız. Birinci otobüsteki yolcuları çift numaralı odaya (yani k1 2 numaralı odaya, k2 4 numaralı odaya) Diğer otobüsteki yolcular ise tek numaralı odaya ( L1 1 numaralı odaya, L2 3 numaralı odaya ) yerleştirilirse tüm yolcular yerleştirilir.
Bu sorunun cevabı bize çift sayıların ve tek sayıların sonsuz sayıda olduğu ve sonsuz bir kümenin alt kümesinin de sonsuz olacağını göstermiştir. (N doğal sayılar kümesi sayılabilir bir sonsuz küme olup 2N ve 2N+1 kümeleri de birer sonsuz sayılabilir kümedir)
Bu soru aslında biz matematikçiler için şunları ifade etti.
- Sonsuz bir sayı olmayıp bir sıfattır. ( Sıfat ne demek? Sayılamayan anlamında nesneyi niteleyen söz öbeği)
- Sonsuz bir sayı olmadığından sonsuz ile sonsuzun toplamı 2.sonsuz değil yine sonsuzdur.
- Çift ve tek sayılar kümesinin bir sonsuz küme olduğunu
- Sonsuz’a ne eklersek ya da çıkarırsak yine sonsuzdur
gibi bulguları daha kavramsal olarak anlamamıza yardım etmiştir.