Yüzyıllar boyunca matematikçiler geometrinin düzlem geometrisi diğer adıyla Öklid geometrisinden oluştuğunu biliyorlardı. Öklid’in “elementler” adlı kitabında 5 postulat’ın olduğunu ve bunlardan 5. postulatın matematikçiler tarafından hep bir karamsar olarak nitelendirilmesi geometri dünyasında çığır açıcı yeni gelişmelere neden olacaktı. 5.belite göre bir noktadan geçen dışındaki bir doğruya paralel, tek bir doğru çizilebilir. Bu ifade birçok müslüman matematikçi tarafından çok iyi ispatlansa da maalesef onların adlarıyla anılmadı.
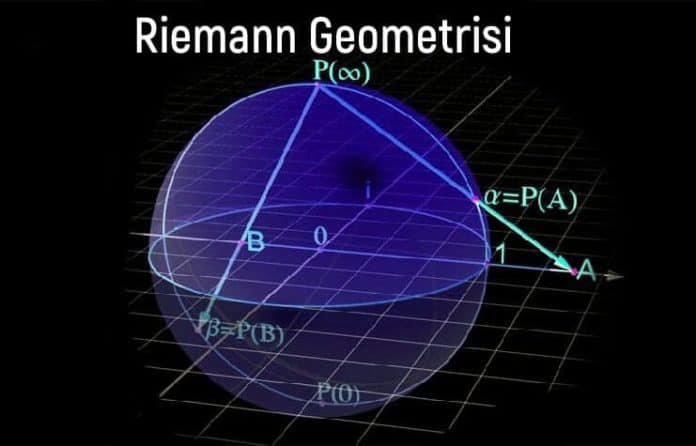
Yıllar 1854’ü gösterdiğinde Alman Matematikçi Bernhard Riemann matematik dünyasını alt üst edecek yeni bir çalışma ortamını keşfetti. Bu “Riemann Geometri” idi. Öklid geometrisinin eksikliği olarak yeni bir geometrik akımının çıkması ilk olarak matematikçiler tarafından iyi karşılanmadı. Bu çok derin ve zor bir konuydu. İlk yazdığı makalede 5. belitin tersini kullanarak şöyle ifade etmiştir; “Bir noktadan dışındaki bir çizgiye hiçbir paralel doğru çizilemez gibi” gibi bir ifade ile kanıtını sunmuştur. Ayrıca Öklid’in başka bir belitini’de (bir doğru parçası doğrusal bir çizgi üzerinde sürekli uzatılabilir) farklı yorumlamıştır. Ona göre doğru bir doğru sınırsızdır fakat sonsuz değildir ama uzunluğu sonludur gibi ifade şekillerini matematik dünyasına sunmuş ve birçok kanıt ile bilimler akademisinden onay almıştır.
Fakat bu söylenen tüm doğru teoremleri kürenin üzerinde göstermek gerektiğini belirtmiştir. İşte Riemann geometrisinin diğer bir adı ise küresel geometri olarak benimsenir. Bunun açık ve net sebebi yapılan çalışmaların bir küre üzerinde yoğunlaşmasındandır. Bir küreyi göz önüne alalım. Kürelerin merkezlerinde iki büyük çemberin kesişimini görebilirsiniz. Bu çemberler sadece iki noktada kesişir. Küresel geometride doğrular iki noktada kesişen büyük çemberlerden başka bir şey değildir. Bu yüzden hiçbir doğru paralel değildir. (Daha fazla ileriye gitmek akademik düzeye çıkılmasına sebebiyet vereceğinden genel manada bilgi vermeyi okuyucuya uygun buluyoruz). Küresel geometride kürenin içinde kesişen iki nokta ve bir de kürenin uç noktası bize bir üçgen oluşturacaktır ama bu üçgenin iç açıları toplamı 180 dereceden büyüktür. Kafamızdaki temel soru şu: Bir üçgenin üçgen olabilmesi için iç açılarının 180 derece olması gerektiğini doğuştan beri biliriz. Peki bu oluşan şekil de neyin nesi? Tabiri caizse gıcır gıcır bir geometrik şekil çıktı diyebiliriz. (Şeklin ne olduğunu, nasıl bir şekil olabileceğini okuyucudan bekliyorum.)
Aslında bu bulunan şey sadece bir geometri dersi için hazırlanmış bilgiler olmasa gerek. Albert Einstein küresel geometri kullanan en önemli kişilikten bir tanesi. Einstein’e göre eğer evrenin kütlesi yeterince büyük ise kütle çekim kuvveti Büyük patlamadan sonra başlayan genişlemeyi durduracaktır. Yani evren büzülüp küresel bir biçim alacaktır. (Derin olduğunu söylemiştik) Ya sonra… Milyarlarca yıl sonra bu küresel evren büzüle büzüle bir nokta haline gelecek ve içinde sonsuz ısı ve yoğunluk olacak yani yoğunlunun sonsuz olması durumuna gelecek. Şayet kütle çekim kuvveti onu büzecek kadar da büyük değilse, belki de o zaman evrenin genişlemesinin durduğu bir denge noktasında ulaşacak.
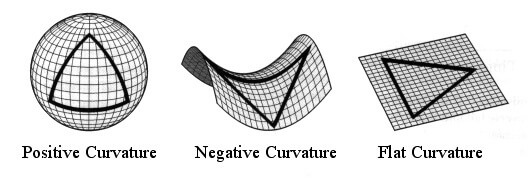Yukarıdan anlayacağımız şey şu: Eğer bilim insanlarının dediği gibi evren sürekli genişler ise Riemann geometrisine göre milyarlarca yıl sonra evren bir küre biçiminde olacaktır. (Kütle çekim kuvvetinin izni ile)