Riemann Hipotezi, ürkütücü bir denklem… Birçok matematikçi için adeta serüven kapısı haline gelmiştir. Bu hipotez Clay Matematik Enstitüsü tarafından “Milyon dolarlık problemler” kategorisinde yer almaktadır. Adından da anlaşılacağı üzere Bernard Riemann (1826 -1866) tarafından ortaya atılmış bir problemdir. Analiz ve diferansiyel geometri de müthiş buluşların sahibidir. Genç yaşında hayatını kaybetmesine rağmen önemli çalışmalar imza atan Riemann, kendi adıyla anılan bu problemi de matematik dünyasına kazandırmıştır. Evet, Riemann Hipotezi çok derin bir konu, sadece bu yazı ile de kalmayacağını çok ama çok iyi bilsek de biraz tartışalım.
Riemann hipotezi veya Riemann Zeta Fonksiyonu kuantum mekaniği ve sayı teorisinin çılgın problemidir. Özellikle asal sayılar hakkında bilgiler veren Zeta fonksiyonu Sayı teoristleri tarafından çözülmeye çalışılmaktadır. Problemi çözdükten sonra alınacak para ne kadar maddi anlamda tatmin edici olsa da prestij anlamında da matematik tarihine kazılacağı kesindir. Riemann hipotezi, Riemann’ın denklemle yaptığı gözlemleri üzerine dayanır. Sıfıra gitmesini sağlayan denklemin her girdi değeri aynı çizgide duruyor gibi gözükür. Bu, bazı okuyucuya ilginç gelmeyecektir fakat bu gözlem net olarak anlaşılabilirse özellikle asal sayıların dağılımı hakkında süper bilgiler verecektir. 150 yıldır (belki de daha fazla) çözülemeyen bu hipotezi şimdi biraz daha derinliklerine inerek inceleyelim. Sıkılmadan…
Riemann Zeta fonksiyonu karmaşık sayılarla ilişkili olduğundan ilk olarak kısa bir karmaşık sayıların özelliklerine bakalım. 11. sınıfta öğrenciler bu konularla biraz haşir neşir oluyorlar. Yıllar önce matematikçiler doğal sayılardan sıkıldıklarından olsa gerek işleri biraz daha karıştırmak için karmaşık sayıları buldular. (Karmaşık sayı “i” ile tanımlanmakta olup, ilk bulunuşu bir denklemin kökünün kök -1 çıkmasından kaynaklanmıştır. Daha sonraları karesi -1 olan sayı olarak kullanılmıştır.) Örneğin; n bir karmaşık sayı olsun ve n=3+i5 biçinde alalım. Burada Reel kısım 3 ve sanal kısım i’nin katsayısı olan 5’tir. Genelde Re(n)=3 ve Im(n)=5 biçiminde gösterilir. Ayrıca doğal sayıları da karmaşık sayı biçimde göstereceğimiz çok açıktır. “34” sayısını ele alalım. Sanal kısmı “0” olduğundan 34+i0 biçimindedir. Bu kadar sıkıcı bilgilerden sonra başlayalım.
Riemann Hipotezi, Riemann zeta fonksiyonun önemsiz olmayan tüm sıfırlarının 0.5 eşit olmadığını söyler. Ne demek yani? Şimdi bir fonksiyon ele alalım. f(x) = x-5 işlevine sahip x=5 bu işlevin ya da fonksiyonun sıfırlarıdır. Riemann Zeta fonksiyonunda da böyle basit sıfırlar var fakat önemli olan zorları bulabilmektir. Fakat o zor sıfırı bulmak bayağı zordur. Ama merak etmeyin Parelman gibi zehirler çözecektir. Önemsiz olmayan sıfırın reel kısmının 0.5 olduğunu söylersek, fonksiyonun dışına çıkan sayı sıfırsa demek ki girdi değerinin gerçek kısmının 0.5 olduğu anlaşılacaktır. İşte Re(s) büyüktür 1 olacaktır.
Ama bir dakika? Eğer zeta fonksiyonu Re(s) büyüktür 1 şeklinde tanımladıysak nasıl olurda reel kısım 0.5 olur? (Hemen Üst Satır) Olamaz! Fakat matematikçiler bunun için “Analitik süreklilik” dediğimiz olay sayesinde öyle bir fonksiyon yapıyoruz ki hem değerlerimiz bozulmuyor hem de reel kısımlar hakkında daha rahat mantık yürütebiliyoruz. Değişen tek şey fonksiyon!
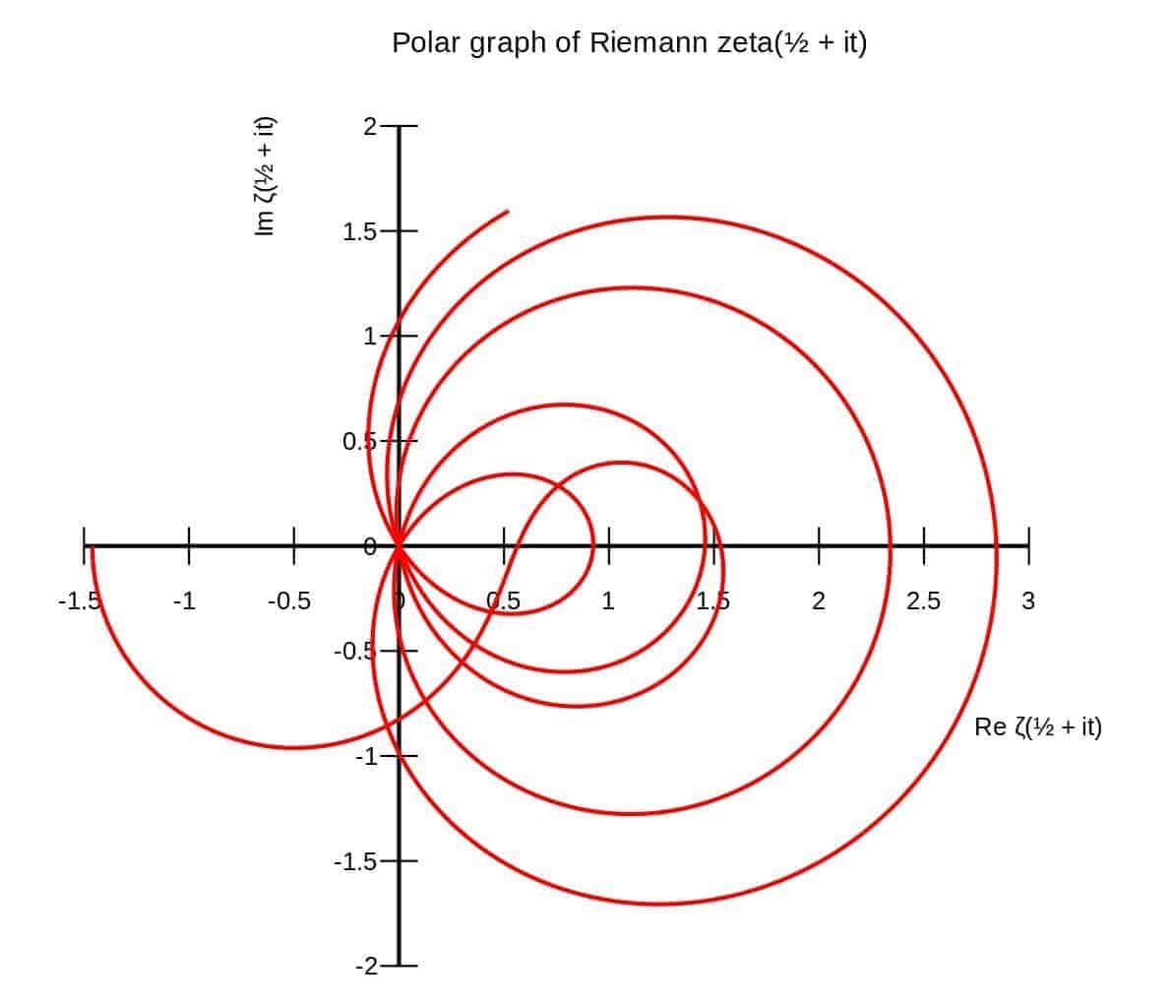İşte tam da bu! Zeta fonksiyonunun grafiğini verelim. Sıfırların nereye düştüğünü görebiliyor musunuz? Yoğunluğun olduğu yer basit şekilde hesaplanan sıfırlardır. Yukarıda sözü geçen zor kelimesi dağılımın seyrek ya da hiç olmadığı yerler için kullanılmıştır.
Riemann hipotezinin önemi işte yoğun yerlere düşen sıfırların bir formülüze edebilmesinin mümkünatı ile ilgilidir. Doğru mudur bilinmez ama Nijeryalı Matematik Profesörü Dr. Opeyemi Enoch tarafından çözüldüğü söylenmektedir fakat son söz Clay Matematik Enstitüsü tarafından verilecektir.
Asıl soru çözümden çok soruyu soran Riemann’ın nasıl bir üst düzey matematikçi olduğudur.