Moleküler dinamik (MD) simülasyonları, silisyum, azot veya bor atomları ile katkılanmış (dopinglenmiş) dikdörtgen biçimdeki grafen tabakalarını gerdirmek (esnetmek) için uygulanmıştır. Young modülü, maksimum gerilim (gerinim) ve enerji absorpsiyonu, katkı konsantrasyonu (DC) % 0–5 arasında değişiklik gösteren grafen levhalar için ölçülmüştür. Burada, her bir katkı maddesinin grafenin temel mekanik özelliklerindeki farklı etkileri üzerinde durulmuştur. Sonuçlar, grafene katkı maddelerini dahil etmenin Young modülünde neredeyse doğrusal bir düşüşe yol açtığını göstermiş, ayrıca maksimum mukavemet, maksimum gerinim ve enerji absorpsiyonundaki tekdüze azalmalar da yine bu çalışmada gözlemlenmiştir. Bu yapılan dopinglerin etkilerinin silisyum için en önemli olduğu, bor için belirgin özelliklerin daha az olduğu ve azot için ise küçük veya ihmal edilebilir olduğu bulunmuştur.
GİRİŞ
Tek atom tabakalı karbon levhalı tek katmanlı grafen, son on yılda iki boyuttaki (2D) kristal yapısı ve sıradışı termal, mekanik ve elektriksel özelliklerinden dolayı oldukça dikkat çekmiştir [1-5]. Benzersiz özellikler nanoelektronikte[6], nanosensörlerde [7], transistorlerde [8] ve nano-kompozitlerde [9]geniş çaplı bir uygulama alanına yol açmıştır. Grafen tabakalarında, topolojik (ilingesel) kusurlar, boşluklar ve katkı maddesinin atomları gibi farklı türlerde atomik ölçek kusurları bulunmuştur [10-12]. Bu kusurların varlığı, grafenin yerel yapıları ve malzeme özellikleri üzerinde önemli bir etki ortaya koyacaktır. Bu etki, orijinal özellikleri uyarlamak ve yeni grafenin meydana gelmesi için yeni bir strateji sağlayacaktır [12-15]. Tipik bir örnek olarak, katkı malzemesinin atomları, nanoaygıtlarda ve nanoelektronikteki uygulamaları için grafenin yarı iletkenlik özelliklerini geliştirmek için etkili biçimde kullanılmıştır [16-17]. Buna ek olarak, grafenin katkısı, işlevselliğini de büyük ölçüde adsorpsiyon özellikleri gibi artıracaktır [18]. Grafenin Silisyum (Si), Azot (N) veya Bor (B) ile katkılanması, karbon atomlarının ideal sp2 hibridizasyonunda (melezleşmesinde) bozulmaya neden olur. Bu yüzden grafenin yerel elektronik, kimyasal ve mekanik özelliklerini önemli ölçüde değiştirir [17,19]. Bu tür bir N katkı mekanizması, grafen elektroniğinin elektronik ve kuantum taşıma özelliklerini modifiye etmek ve grafen sensörlerinin biyouyumluluğunu ve duyarlılığını artırabilmek amacıyla başarı bir şekilde kullanılmıştır [16,20–22].
Ancak, katkı malzemesi atomlarının yerlerinin değiştirilmesi, grafenin mükemmel mekanik özelliklerini geriletebilir ve grafen bazlı nanoaygıtların ve nanoelektroniklerin performansını etkileyebilir. Bu nedenle yapılan katkının grafenin mekanik özellikleri üzerindeki etkisini değerlendirmek oldukça ilgi çekici olmaktadır. Şimdiye kadar, atom kusurlarının ve yapılan katkının mekanik özelliklere genel etkilerini incelemek için bazı çabalar gösterilmiş olmasına rağmen [23-25], mevcut katkı malzemelerinin etkilerindeki – örneğin B, N ve Si’nin grafenin mekanik özellikleri ve özellikle deformasyon mekanizması üzerindeki etkilerindeki – farklılık dopinglenmiş grafen levhaların oldukça önemli olan pratik uygulamaları üzerinde hala detaylı olarak çalışma yapılamamıştır.
Bu çalışmada, moleküler dinamik (MD) simülasyonları esaslı silisyum, bor ve azot katkılarının tek katmanlı grafen levhaların mekanik özelliklerine etkilerini araştırdık. Burada B, N ve Si katkı malzemelerinin grafenin Young modülü ve maksimum çekme mukavemeti (gerinim/enerji) üzerindeki etkileri tartışıldı ve nicel olarak birbirleriyle karşılaştırıldı.
MOLEKÜLER DİNAMİK SİMÜLASYONU
Bu çalışmada, bozulmamış ve dopinlenmiş grafen levhaların gerilme testleri, moleküler dinamik simülasyonları göz önüne alınarak gerçekleştirildi ve Sandia National Laboratories tarafından geliştirilen LAMMPS (Large-Scale Atomic/Molecular Massively Parallel Simulator) açık kaynaklı paket [26] kullanıldı. Burada MD modelinin doğruluğu, dikkate alınan atom yapıları için seçilen atomlararası potansiyellere önemli ölçüde bağlıdır. Bu çalışmada, bozulmamış grafenin atomlararası etkileşimlerini tanımlayabilmek için Tersoff potansiyeli [27,28] kullanıldı. Böyle bir potansiyel özel olarak karbon bazlı sistemler için doğru olarak tasarlanmış ve kanıtlanmıştır, örneğin grafit, elmas, fulerinler ve nanotüpler gibi [29-31]. Karbon bazlı sistemler için Tersoff potansiyelinin eşsiz özelliği, kısa mesafede bağlı etkileşimlerin reaktif olmasıdır. Sonuç olarak, kimyasal bağlar simülasyonların seyri sırasında oluşabilir ve kopabilir. Bununla birlikte, farklı atomlar ile katkılanmış grafen tabakaları için farklı atom-altı potansiyeller kullanılmış olmasına rağmen, şimdiye kadar katkılı grafen modellemesinde birleştirilmiş bir atomlararası potansiyel mevcut değildir [27,28,32-36].
Böylece önceki çalışmaları takiben, bireysel atomlarla katkılanmış grafen için spesifik atomlararası potansiyeller seçildi. Burada Si katkılı grafende orijinal Tersoff potansiyeli [27,28] C-C ve C-Si bağları için kullanıldı. B ve N katkılı grafen levhalarında ise optimize edilmiş Tersoff potansiyeli [32] C-C bağları için uygulanmış ve Ref. 33’te geliştirilen potansiyel, C-B ve C-N bağları için kullanılmıştır. Daha sonra görülebileceği gibi, farklı atomlararası potansiyellerin kullanılması elde edilen sonuçlar arasında tutarsızlıklara yol açabilmektedir. Diğer yandan grafen levhalarının mekanik davranışlarını karakterize eden seçilmiş potansiyelleri karşılaştırmamız için de iyi bir fırsat sunuyor.
Bu çalışmada örnek levhalar olarak kullanılan dikdörtgen bozulmamış ve katkılı grafen levhaların şemaları Şekil 1’de gösterilmiştir. Model, boyutları 84 °A × 75 °A civarlarında.olan 2440 atomdan oluşmaktadır. Katkı maddelerinin yer değiştirilmesi, karbon atomlarının rastgele Si, B veya N atomlarıyla değiştirilmesi ile gerçekleştirildi. Katkı konsantrasyonu (DC), orijinal bozulmamış grafen levhasının toplam atom numarasının katkı atom numarasına oranı ile tanımlanmıştır. Yer değiştirme işlemi sırasındaki katkı atomu arasında kimyasal bağların (örneğin Si-Si bağları arasındaki kimyasal bağların) oluşması engellenmiştir.
Bu mevcut çalışmada, numunelerin mekanik özelliklerini ölçmek için çekme (gerilme) testleri uygulandı.Yükleme uygulanmadan önce, grafen tabakalarının konfigürasyonu, eşlenik gradyen yöntemi kullanılarak optimize edildi. Bu yöntem aracılığıyla, numune tamamen rahatlatıldı ve minimum iç enerji ile ilişkili denge durumuna getirildi.Daha sonra, optimize edilmiş levhaları koltuk yönünde uzatmak için bir tek eksenli gerilme uygulanmıştır (Şekil 1’de gösterildiği gibi x yönü).Gerinim oranının, grafen, karbon nanotüpleri ve h-BN nanotabakaları içeren nanomalzemelerin mekanik özellikleri üzerindeki etkileri dikkat çekici bir noktadır [37-42]. Önceki çalışmalarımızda [37,38], yükleme oranı kritik bir değerden (108-109civarında) düşük olduğunda, gerinim oranı etkisi önemsiz ve dolayısıyla güvenli bir şekilde ihmal edilebilir bulunmuştu. Bu nedenle, hesaba dayalı fizibilite için, MD simülasyonlarında genellikle 109civarı gerinim oranı kullanılmaktadır. Bu çalışmada mühendislik gerinim oranı 1×109 s-1‘de kontrol edildi ve zaman1.0 fs (femtosaniye-saniyenin katrilyonda biri) olarak ayarlandı.Sınırlı uzunluk etkilerini ortadan kaldırmak için ise yükleme yönü boyunca periyodik sınır koşulları (PBC) uygulandı.Bu koşullar, ayrıca, genişlik yönü boyunca (yani, Şekil 1’de gösterildiği gibi Y yönü) uygulandı ve bu da, sonsuz genişlikli grafen levhalarının simülasyonlarda karakterize edildiğini gösterdi.
Newton’un hareket denklemleri, Hız-Verlet algoritması [43] kullanılarak bütünleştirildi. Bireysel olarak simülasyonlarda sıcaklık, Nose-Hoover metodu kullanılarak sabit tutuldu [44,45].Mühendislik gerilme-şekil değiştirme eğrilerini elde etmek için her gerinim seviyesinde yükleme yönündeki viral gerilimler hesaplandı.Young modülü, düşük gerilme seviyelerinde gerilme-gerinim eğrisinin doğrusal kısmının eğimi olarak hesaplandı.Maksimum gerilme mukavemeti ve maksimum çekme gerinimi, gerilimin maksimum değere ulaştığı noktada ölçüldü.
Enerji absorpsiyonu, gerilme-gerinim eğrilerini 0’dan maksimum gerinime kadar olan gerinme aralığına entegre ederek ölçüldü. Burada grafen levhalarının eşdeğer Young modülünün efektif kalınlığı ile ölçeklendirilmiş olduğunu belirtmek gerekir. Diğer bir ifadeyle, Young modülünün spesifik değeri, seçilen efektif kalınlık ile ilişkilendirildi. Bu çekme testinde, daha önceki çalışmalara uygun olarak, grafitin ara tabakası aralığı (0.335 nm) efektif kalınlık olarak kabul edilmiştir [46-48].Bununla birlikte, bu efektif kalınlığın, bükülme sertliğinin hesaplanmasında büyük hatalara yol açabileceği için grafenin bükülmesi için uygulanabilir (uygun) olmadığı dikkat edilmesi gereken önemli bir noktadır [4,49].
III. SONUÇLAR VE TARTIŞMA
MD simülasyonuna bağlı olarak çekme testleri sırasıyla Si, N ve B ile katkılanmış grafen levhaları üzerinde uygulandı. Bu esnada gerilme-gerinim eğrilerinin % 0’dan (bozulmamış grafenden) % 5’e artışı grafen tabakaları için DC ile kaydedildi. Veriler, Şekil 2’de Si atomları ile katkılanmış grafen için gösterilmiştir. Stres – gerinim eğrilerinden, incelenen grafen için Young modülü, maksimum dayanım, maksimum gerinim ve enerji absorpsiyonu çıkarılmıştır. DC üzerindeki bu anahtar malzeme özelliklerinin bağımlılıkları, dikkate alınan tüm grafen tabakaları için Şekil 3’te grafikle çizilmiştir.
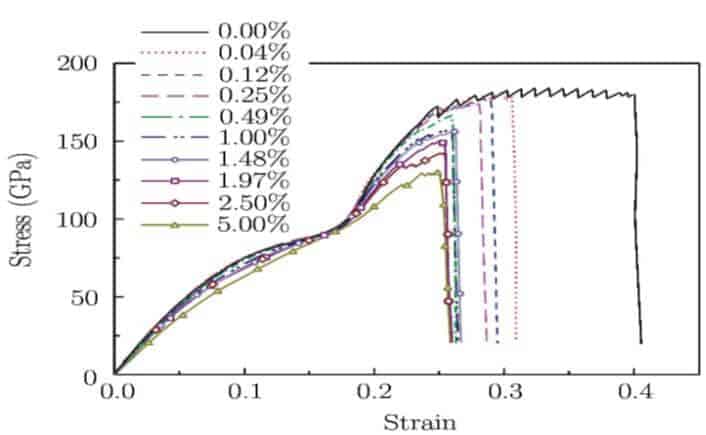
Şekil 2, tek eksenli gerilim altındaki Si katkılı grafen levhaların genel gerilme tepkilerini göstermektedir. Şekil 2’de gösterildiği gibi, ilk olarak bozulmamış grafenin gerilimi, gerinim yavaş yavaş % 25’e yükseldiğinde artmaktadır. Doğrusal gerilme-gerinim ilişkisi % 3’ün altında küçük gerinimde bulunur. Gerinim % 25’in üzerinde olduğunda gerilimin arttığı gözlemlenir. Gerilimin % 25 ila % 40 arasında değiştiği zaman ise akma platformu gözlemlenir ki bu neredeyse sabit bir değere hafifçe düşen bir platformdur. Diğer bir ifadeyle, grafen levhaya bağlı atomlar sürekli olarak neredeyse sabit bir gerilme ile akar.Bundan hemen sonra, ani bir gerilim sıçraması, neredeyse değişmeyen bir gerinim ortaya çıkarır ve grafenin kırılmasını gösterir. Bozulmamış grafenin böyle bir gerilme tepkisi, Si atomlarını grafen tabakalarına dahil ederek önemli ölçüde değiştirilebilir.
Şekil 2’de, katkılı grafenin geriliminin, herhangi bir akma platform olmadan büyüyen gerinme ile arttığı gözlemlenmiştir. Dahası, Şekil.2’de doğrusal gerilme-gerinme ilişkisi daha yüksek Si DC ile dopinglenmiş grafen tabakaları için daha geniş bir gerinim aralığında bulunmuştur.Örneğin, doğrusal gerilme – gerinim ilişkisiyle bağlı maksimum gerilme, DC <% 0.5’de 0.05’den düşüktür ama, DC % 5’e yükseltildiğinde bu değer yaklaşık 0.15 – 0.25’e yükselmektedir.Bu, daha yüksek Si DC’li Si katkılı grafenin, geniş bir gerinim aralığında doğrusal bir elastik materyal olduğunu gösterir.Öte yandan bozulmamış grafen için gözlemlenen akma platformu (DC yükselirken veya DC % 5’e ulaştığında tamamen kaybolduğunda) daha kısa olur, yada diğer bir deyişle yüksek Si DC’li katkılı grafen, çekme gerilimini maksimum değere ulaştırır. Simülasyonlar , N- ve B- katkılı grafenin de genel çekme tepkilerinin nitel olarak Şekil 2’de gösterilen Si-katkılı grafene benzer olduğunu göstermektedir.
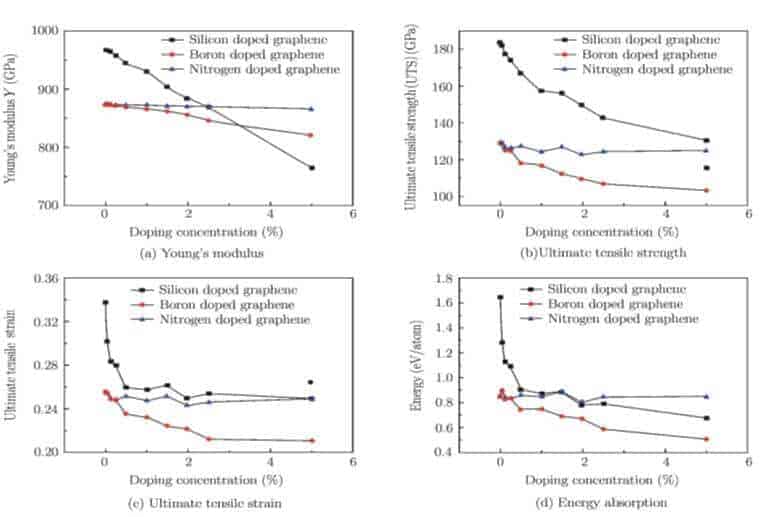
Şekil 3 (a) ve 3 (b) silisyumun çeşitli katkı konsantrasyonlarına sahip Si, N ve B katkılı grafenin Young modülünün ve maksimum dayanımının eğilimini göstermektedir. Burada bozulmamış grafen için elde edilen Young modülü yaklaşık 0.87 TPa – 1.0 TPa’dır ve başlangıçtan itibaren (ab initio) hesaplamaları ve MD simülasyon sonuçları ile iyi bir şekilde uyum içindedir [50-52], ve bu yaklaşık 1.0 TPa’lık deneysel sonuçları ile de uyumludur [4].Sonuç olarak elde edilen 130 GPa’lık akma mukavemeti, MD simülasyonları (121 GPa) [52] ve yapılan deney (130 GPa) [4] baz alınarak elde edilen önceki verilerle de iyi bir uyum içindedir. Bu çalışma ile yapılan deneyler arasında iyi bir uyuşma elde edilmiş ve atomistik simülasyonlar mevcut MD simülasyonlarının güvenilirliğini doğrulamıştır.
Bölüm 2’de de bahsedildiği gibi MD modellemesinin doğruluğu, dikkate alınan atomik yapılar için seçilen atomlararası potansiyellere bağlıdır. Bu çalışmada, saf grafen tabakasının gerilim-gerinim eğrisi varsayılan parametrelerle Tersoff potansiyeli baz alınarak elde edilmiştir. Tersoff potansiyeline bağlı olarak elde edilen bozulmamış grafenin materyal özellikleri literatürde bildirilenlerle mükemmel bir şekilde uyumlu bulunmuştur. Öte yandan Ref. [53]’te ve Tersoff potansiyelinin kullanıldığı mevcut çalışmada, bozulmamış grafenin MD simülasyonlarında bir gerinim sertleştirme aşaması elde edilmiştir. Ancak bu sertleşme, deneylerde [4] ve baştan itibaren yapılan (ab initio) hesaplamalarda [50] gözlemlenmemiştir.
Yazarlar, ‘gerinim sertleştirme’ sorununun kullanılan spesifik potansiyel fonksiyondan kaynaklanabileceğine ve yakın zamanda geliştirilmiş potansiyellerin, örneğin değiştirilmiş kesme değerlerine sahip REBO veya AIREBO potansiyelinin kullanılması ile çözülebileceğine inanmaktadırlar. Ne yazık ki, REBO ya da AIREBO, bu çalışmada kolaylıkla kullanılamamaktadır, çünkü birkaç farklı kimyasal bağın bulunduğu katkılanmış grafen ile başa çıkamıyor olabilme ihtimali vardır.Şekil 3 (a) ve 3 (b) ‘den açıkça görüldüğü üzere, Si katkılı grafenin Young modülü ve maksimum dayanımı, Si atomlarının artan DC’si ile monoton bir şekilde azalmaktadır.Diğer bir ifadeyle, Si katkılı grafen genellikle bozulmamış grafenden daha yumuşak ve zayıftır.
Özellikle, Young modülünün, Si DC ile hemen hemen doğrusal bir ilişkiye sahip olduğu ve DC % 1’e yükseltildiğinde (mutlak büyüme) 35 GPa civarına azaldığı belirtilmektedir.Şekil 3 (a) ‘da gösterildiği gibi, böyle bir değişim oranı en sonunda Si’nin DC’si % 0’dan % 5’e değiştiği için Young modülünde yaklaşık % 20.9’luk bir düşüşe yol açar.Şekil 3 (b) ‘deki maksimum mukavemet için, DC = 0’da 183.5 GPa’dan DC = %5’te 130.6 GPa’ya, göreceli olarak yaklaşık % 28.9’luk oranla azalan maksimum mukavemet için önemli değişim görülür.
Şekil 3 (a) ‘da görüldüğü gibi, Si katkılı grafene benzer şekilde, Young modülü N ve B katkılı grafen artan DC ile doğrusal olarak azalmaktadır. DC’nin % 0’dan % 5’e yükseldiği proseste, Si katkılı grafen için hesaplanan % 20.9’dan küçük olan B katkılı grafen için % 9.5 düşüş gözlemlenir. Fakat N-katkılı grafen için bu değer % 1.4’ten daha fazla olmuştur. Dolayısıyla, N katkı malzemelerinin grafenin Young modülüne etkisi neredeyse önemsizdir. Buna ek olarak, Şekil 3 (b) ‘de, Si katkısıyla ilişkili eğilimden farklı olarak, N veya B atomlarının DC’si kritik bir değere yükseldikçe (N atomları için% 2 ve B atomları için % 10) maksimum mukavemet azalmaktadır. Ancak DC’nin daha da artması, grafen levhanın maksimum dayanımını yükseltir. Verilen bir DC için, N-katkılı grafenin maksimum mukavemeti, B-katkılı grafenden daha büyüktür.Burada B katkı maddelerinin etkisi genellikle N katkı maddesininkinden daha belirgin olarak bulunur.
Şekil 3 (c) ve 3 (d) ‘de, Si katkılı grafenin maksimum gerinimi ve enerji absorpsiyonu için DC ile monoton değişiklikler de aynı zamanda gözlemlenmiştir. Maksimum gerinim ve enerji absorpsiyonu artan DC ile azalır. DC’nin küçük bir artışının bir sonucu olarak (yani, 0’dan 0.05’e kadar), maksimum gerinim % 26 oranında azalır (0.33’den 0.25’e) ve enerji absorpsiyonu% 59 oranında azalır (1.64’den 0.68 eV / atom’a). İlk aşamadaki düşüş önemlidir, bu da grafenin mekanik özelliklerinin, katkı atomlarının yoğunluğu çok düşük olduğunda katkıya karşı çok hassas olduğunu gösterir. Buradan yüz milyonlarca ev sahibi atom arasında sadece bir tane katkı atomunun, ev sahibi materyalin fiziksel özelliklerini önemli ölçüde değiştirebildiği anlaşılmaktadır. Bununla birlikte DC,% 5’e yükseltildiğinde, maksimum gerinim ve enerji absorpsiyonunun hemen hemen değişmeden kaldığı duyarsız bir eğilim elde edilir. Bu sonuç, DC’nin düşük maksimum gerinim (veya enerji absorpsiyonu) ile bağlantılı kritik değeri aştığında, maksimum gerinimin (veya enerji absorpsiyonunun) DC değişimine karşı daha az duyarlı hale geldiğini açıkça göstermektedir.
Şekil 3 (c)’de gösterildiği gibi N ve B katkılı grafenler için, DC arttıkça, B katkılı grafenin maksimum gerinimi, Si katkılı grafenin için gözlemlenen büyük sıçramanın keskin kontrastında yalnızca çok az azalmaktadır. B katkılı grafenin aksine, N katkılı grafenin maksimum gerilimi DC’nin artmasıyla hemen hemen sabit kalır.Ayrıca, Şekil 3 (d)’de, B-katkılı grafen için elde edilen enerji absorpsiyonu, maksimum gerinime benzer bir DC-bağımlılığı göstermektedir (Şekil 3 (c)). Oysa N katkılı grafenin enerji absorpsiyonu sadece neredeyse sabit bir değer etrafında biraz dalgalanma yapar ve bu da N-katkısının grafenin enerji absorpsiyonunu önemli ölçüde değiştirmediğini gösterir.
Şekil 4’te de gösterildiği gibi, farklı katkı atomlarının grafenin deformasyon mekanizması üzerindeki etkisini de inceledik. Şekil 4 (a) – 4 (c)’de görelebildiği gibi, N ve B katkılı grafen levhaları ile karşılaştırıldığında, Si katkılı grafen tabakasının gevşemeden sonra, özellikle katkılı atomların bulunduğu lokasyonlar civarında daha belirgin buruşukluklara sahip olduğu görülebilir. Yazarlara göre katkı etkisi ağırlıklı olarak karbon atomları ile katkı atomları arasında oluşan kimyasal bağlar tarafından ve geometrik boyut ile belirlenir.Bu özel durumda, Si ve C atomları arasındaki yarıçap farkı B / N ve C arasındaki değerden çok daha büyüktür ve bu da sonunda katkılanmış grafen levhaların mekanik özelliklerinde çok ciddi azalmalara yol açabilir. Katkı yaparak oluşturulan kimyasal bağlardaki değişiklikleri açıklamak için daha ileri çalışmalara ihtiyaç vardır.
İlk kusurların veya boşlukların çekirdeklenmeleri oluştuğunda Si-, N- ve B-katkılı grafen levhalarının deformasyonları sırasıyla olacak şekilde Şekiller 4 (d), 4 (e) ve 4 (f) ‘de gösterilmektedir. Bozulmamış grafene benzer şekilde, katkılı grafen de yükleme yönü boyunca üniform olarak uzanır (genişler). Bununla birlikte, bu üç atom ile katkılanmış grafen levhaların deformasyon mekanizmaları farklıdır. Şekil 4 (d) ‘de gösterildiği gibi, Si katkılı grafende, ilk başlangıçtaki kusurlar, içte uzayan ve numune genişliği (eni) boyunca zayıf bir bölge oluşturan bölgede oluşmuş gibi gözükmektedir. Buna ek olarak, bu başlangıç kusurlarına iki komşu karbon atomu yerine iki komşu karbon ve silisyum atomu arasındaki bağ açılmasının (debonding) neden olduğu düşünülmektedir.
Şekil 4 (e) ve 4 (f) ‘de gösterildiği gibi Si katkılı grafenden farklı olarak, N- ve B-katkılı grafenin ilk başlangıçtaki kusurları, grafen levhalarının kenarına yakın olarak oluşturulmuştur ve bu grafen levhaları, bozulmamış grafen levhalarına benzerdir [54].Bu noktada, N katkısının ve B katkısının, grafenin bu mekanik özellikleri üzerinde neredeyse hiçbir etkisi olmadığı anlaşılmaktadır. Burada, yukarıdaki sonuçların sadece koltuk grafen levhaları için elde edildiğini belirtmek oldukça önemlidir. Olası kiralite (chirality) bağımlılığını incelemek için zigzaglı grafen levhalar üzerinde de gerilme testler yapıldı. Grafenin mekanik özelliklerindeki benzer katkı etkileri gözlemlendi, bu da aynı şekilde kiralite etkisinin de çok önemli (kayda değer) olmadığını göstermiş oldu.

- SONUÇLAR
Bu çalışmada, grafen levhaların mekanik özellikleri açısından Si, N ve B katkı etkileri incelenmiştir. MD simülasyonunun çekme testleri, katkı konsantrasyonu % 0’dan % 5’e artan dikdörtgen grafen levhalar üzerinde gerçekleştirilmiştir. Sonuçlar, katkı maddesinin (Si, N veya B) grafene dahil edildiğinde, Young modülünde neredeyse doğrusal bir düşüşe neden olduğunu göstermektedir. Maksimum mukavemet, maksimum gerinim ve enerji absropsiyonunda monoton (tekdüze) düşüşler de gözlenmiştir. Bu yapılan katkı etkilerinin silisyum için en belirgin olduğu, bor için daha az belirgin olduğu ve azot için ise küçük veya ihmal edilebilir ve önemsiz olduğu bulunmuştur.
Bu makale ScienceDirect aracılığı ile alınmış olup çevirisi Mustafa Yunus KAYA tarafından yapılmıştır.
sciencedirect.com/science/article/pii/S0894916616300039 Son Erişim: Aralık 2017
REFERANSLAR
[1] Novoselov,K.S., Geim,A.K., Morozov,S.V., Jiang,D., Zhang,Y., Dubonos,S.V., et al., Electric field effect in atomically thin carbon films. Science, 2004, 306(5696): 666-669.
[2] van den Brink,J., Graphene: from strength to strength. Nature Nanotechnology, 2007, 2(4): 199-201.
[3] Geim,A.K. and Novoselov,K.S., The rise of graphene. Nature Materials, 2007, 6(3): 183-191.
[4] Lee,C., Wei,X., Kysar,J.W. and Hone,J., Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science, 2008, 321(5887): 385-388.
[5] Balandin,A.A., Ghosh,S., Bao,W., Calizo,I., Teweldebrhan,D., Miao,F., et al., Superior thermal conductivity of single-layer graphene. Nano Letters, 2008, 8(3): 902-907.
[6] Areshkin,D.A. andWhite,C.T., Building blocks for integrated graphene circuits. Nano Letters, 2007, 7(11): 3253-3259.
[7] Brownson,D.A.C. and Banks,C.E., Limitations of CVD graphene when utilised towards the sensing of heavy metals. Rsc Advances, 2012, 2(12): 5385-5389.
[8] Schwierz,F., Graphene transistors. Nature Nanotechnology, 2010, 5(7): 487-496.
[9] Novoselov,K.S., Fal’ko,V.I., Colombo,L., Gellert,P.R., Schwab,M.G. and Kim,K., A roadmap for graphene. Nature, 2012, 490(7419): 192-200.
[10] Hashimoto,A., Suenaga,K., Gloter,A., Urita,K. and Iijima,S., Direct evidence for atomic defects in graphene layers. Nature, 2004, 430(7002): 870-873.
[11] Meyer,J.C., Kisielowski,C., Erni,R., Rossell,M.D., Crommie,M.F. and Zettl,A., Direct imaging of lattice atoms and topological defects in graphene membranes. Nano Letters, 2008, 8(11): 3582-3586.
[12] Carr,L.D. and Lusk,M.T., Defect engineering: Graphene gets designer defects. Nature Nanotechnology, 2010, 5(5): 316-317.
[13] He,L.C., Guo,S.S., Lei,J.C., Sha,Z.D. and Liu,Z.S., The effect of Stone-Thrower-Wales defects on mechanical properties of graphene sheets—a molecular dynamics study. Carbon, 2014, 75: 124-132.
[14] Sha,Z.D., Pei,Q.X., Liu,Z.S., Shenoy,V.B. and Zhang,Y.W., Is the failure of large-area polycrystalline graphene notch sensitive or insensitive? Carbon, 2014, 72: 200-206.
[15] Sha,Z.D., Quek,S.S., Pei,Q.X., Liu,Z.S., Wang,T.J., Shenoy,V.B., et al., Inverse pseudo hall-petch relation in polycrystalline graphene. Scientific Reports, 2014, 4: 5991.
[16] Riedl,C., Coletti,C. and Starke,U., Structural and electronic properties of epitaxial graphene on SiC(0001): a review of growth, characterization, transfer katkı and hydrogen intercalation. Journal of Physics D—Applied Physics, 2010, 43(37): 374009.
[17] Guo,B.D., Liu,Q.A., Chen,E.D., Zhu,H.W., Fang,L.A. and Gong,J.R., Controllable N-katkı of graphene. Nano Letters, 2010, 10(12): 4975-4980.
[18] Chi,M. and Zhao,Y.P., Adsorption of formaldehyde molecule on the intrinsic and Al-doped graphene: a first principle study. Computational Materials Science, 2009, 46(4): 1085-1090.
[19] Wang,X.R., Li,X.L., Zhang,L., Yoon,Y., Weber,P.K., Wang,H.L., et al., N-Katkı of graphene through electrothermal reactions with ammonia. Science, 2009, 324(5928): 768-771.
[20] Lv,R.T. and Terrones,M., Towards new graphene materials: doped graphene sheets and nanoribbons. Ma- terials Letters, 2012, 78: 209-218.
[21] Lv,R., Li,Q., Botello-Mendez,A.R., Hayashi,T., Wang,B., Berkdemir,A., et al., Nitrogen-doped graphene: beyond single substitution and enhanced molecular sensing. Scientific Reports, 2012, 2: 586.
[22] Wang,Y., Shao,Y.Y., Matson,D.W., Li,J.H. and Lin,Y.H., Nitrogen-doped graphene and its application in electrochemical biosensing. Acs Nano, 2010, 4(4): 1790-1798.
[23] Mortazavi,B., Ahzi,S., Toniazzo,V. and Remond,Y., Nitrogen katkı and vacancy effects on the mechanical properties of graphene: a molecular dynamics study. Physics Letters A, 2012, 376(12-13): 1146-1153.
[24] Mortazavi,B. andAhzi,S.,Molecular dynamics study on the thermal conductivity and mechanical properties of boron doped graphene. Solid State Communications, 2012, 152(15): 1503-1507.
[25] Zheng,Q.B., Li,Z.G. and Yang,J.H., Effects of N katkı and NH2 grafting on the mechanical and wrinkling properties of graphene sheets. Rsc Advances, 2013, 3(3): 923-929.
[26] Plimpton,S., Fast parallel algorithms for short-range molecular-dynamics. Journal of Computational Physics, 1995, 117(1): 1-19.
[27] Tersoff,J., Modeling solid-state chemistry: interatomic potentials for multicomponent systems. Physical Review B: Condensed Matter and Materials Physics, 1989, 39(8): 5566-5568.
[28] Tersoff,J., Erratum: modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Physical Review B: Condensed Matter and Materials Physics, 1990, 41(5): 3248.
[29] Bu,H., Chen,Y.F., Zou,M., Yi,H., Bi,K.D. and Ni,Z.H., Atomistic simulations of mechanical properties of graphene nanoribbons. Physics Letters A, 2009, 373(37): 3359-3362.
[30] Mortazavi,B., Remond,Y., Ahzi,S. and Toniazzo,V., Thickness and chirality effects on tensile behavior of few-layer graphene by molecular dynamics simulations. Computational Materials Science, 2012, 53(1): 298-302.
[31] Gupta,S., Dharamvir,K. and Jindal,V.K., Elastic moduli of single-walled carbon nanotubes and their ropes. Physical Review B: Condensed Matter and Materials Physics, 2005, 72(16): 165428.
[32] Lindsay,L. and Broido,D.A., Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Physical Review B: Condensed Matter and Materials Physics, 2010, 81: 205441.
[33] Kinaci,A., Haskins,J.B., Sevik,C. and Cagin,T., Thermal conductivity of BN-C nanostructures. PhysicalReview B: Condensed Matter and Materials Physics, 2012, 86(11): 115410.
[34] Matsunaga,K., Fisher,C. and Matsubara,H., Tersoff potential parameters for simulating cubic boron carbonitrides. Japanese Journal of Applied Physics Part 2—Letters, 2000, 39(1ab): L48-L51.
[35] Moon,W.H., Son,M.S. and Hwang,H.J., Molecular-dynamics simulation of structural properties of cubic boron nitride. Physica B—Condensed Matter, 2003, 336(3-4): 329-334.
[36] Stuart,S.J., Tutein,A.B. and Harrison,J.A., A reactive potential for hydrocarbons with intermolecular interactions. Journal of Chemical Physics, 2000, 112(14): 6472-6486.
[37] Han,T.W., He,P.F., Wang,J., Zheng,B.L. and Wu,A.H., Strain rate dependences of tensile failure process for single graphene sheet: a molecular dynamics study. Science in China Series G: Physics, Mechanics, Astronomy, 2009, 39(9): 1312-1319.
[38] Han,T.W., Luo,Y. and Wang,C.Y., Effects of temperature and strain rate on the mechanical properties of hexagonal boron nitride nanosheets. Journal of Physics D—Applied Physics, 2014, 47(2): 025303.
[39] Chen,M.Q., Quek,S.S., Sha,Z.D., Chiu,C.H., Pei,Q.X. and Zhang,Y.W., Effects of grain size, temperature and strain rate on the mechanical properties of polycrystalline graphene—a molecular dynamics study. Carbon, 2015, 85: 135-146.
[40] Dumitrica,T., Hua,M. and Yakobson,B.I., Symmetry-, time-, and temperature-dependent strength of carbon nanotubes. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(16): 6105-6109.
[41] Dumitrica,T. and Yakobson,B.I., Strain-rate and temperature dependent plastic yield in carbon nanotubes from ab initio calculations. Applied Physics Letters, 2004, 84(15): 2775-2777.
[42] Zhao,H. and Aluru,N.R., Temperature and strain-rate dependent fracture strength of graphene. Journal of Applied Physics, 2010, 108(6): 064321.
[43] Swope,W.C., Anderson,H.C., Berens,P.H. and Wilson,K.R., A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: application to small water clusters. The Journal of Chemical Physics, 1982, 76(1): 637-649.
[44] Nose,S., A molecular dynamics method for simulation in the canonical ensemble. Molecular Physics, 1984, 52(2): 255-268.
[45] Hoover,W.G., Canonical dynamics: Equilibrium phase-space distributions. Physical Review A, 1985, 31(3): 1695-1697.
[46] Lee,C., Wei,X.D., Kysar,J.W. and Hone,J., Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science, 2008, 321(5887): 385-388.
[47] Gupta,A., Chen,G., Joshi,P., Tadigadapa,S. and Eklund,P.C., Raman scattering from high-frequency phonons in supported n-graphene layer films. Nano Letters, 2006, 6(12): 2667-2673.
[48] Salvetat,J.P., Bonard,J.M., Thomson,N.H., Kulik,A.J., Forro,L., Benoit,W., et al., Mechanical properties of carbon nanotubes. Applied Physics A—Materials Science & Processing, 1999, 69(3): 255-260.
[49] Wang,C.Y. and Zhang,L.C., A critical assessment of the elastic properties and effective wall thickness of single-walled carbon nanotubes. Nanotechnology, 2008, 19(7): 075705.
[50] Liu,F., Ming,P.M. and Li,J., Ab initio calculation of ideal strength and phonon instability of graphene under tension. Physical Review B: Condensed Matter and Materials Physics, 2007, 76(6): 064120.
[51] Zang,J.L., Yuan,Q.Z.,Wang,F.C. and Zhao,Y.P., A comparative study of Young’s modulus of single-walled carbon nanotube by CPMD, MD and first principle simulations. Computational Materials Science, 2009, 46(3): 621-625.
[52] Pei,Q.X., Zhang,Y.W. and Shenoy,V.B., A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene. Carbon, 2010, 48(3): 898-904.
[53] Ni,Z.H., Bu,H., Zou,M., Yi,H., Bi,K.D. and Chen,Y.F., Anisotropic mechanical properties of graphene sheets from molecular dynamics. Physica B—Condensed Matter, 2010, 405(5): 1301-1306.
[54] Han,T.W., He,P.F.,Wang,J. and Zheng,B.L.,Molecular dynamics simulation of single graphene sheet under tension. New Carbon Materials, 2010, 25(4): 261-266

