İslam dönemi matematiğini anlatmaya başlamadan önce açıkça söylemekte fayda bulduğumuz bir nokta var. Matematik ve bilim İslam dünyasının temelidir. Kutsal kitabında “Oku” ile başlayan kelime bulunan bir din, bilim ve matematikten yoksun olabilir mi? Açıkça bir cevap verebiliriz. Tabi ki hayır… Bilimin merkezi olan İslam dünyası (maalesef şimdi değil) birçok bilim insanını çıkarmıştır. Matematik dünyası ise İslam bilim tarihine çok şey borçludur. 750 yılından sonra Abbasiler ile birlikte bilim canlandı. Özellikle başkentin Şam değil de Bağdat yapılması konum itibari ile de avantaj sağlamıştır. Yunan medeniyetinde “Museum” adı verilen bilim merkezlerine benzer olarak kurdukları “Dar’ül Hikmet – Aklın evi” ile birlikte bölgenin en büyük çeviri merkezi ve üniversitesini kurmuşlardır. Başta Yunan medeniyetine ait yunanca eserleri çevirmeye başlamışlar daha sonra bölgeye gelen çevirmenler ile birlikte başka dillerin eserlerini de çevirmeye başlamışlardır.
5000’in üzerinde yapılan çeviriler ile birlikte bölgenin bilimsel faaliyetlerini arttırmak adına büyük bir kütüphane kuruldu. İslam bilginleri sadece Yunan medeniyetine ait kitapları değil, Hint ve Mezopotamya medeniyetlerine ait kaynakları da çevirdiğinden dolayı o döneme kadar olan matematik bilgilerinin hepsine vakıf olmuştur. Şu çok önemli bir noktadır ki eski tarihte bilim insanlarının sadece bir dal ile kalmayıp birçok bilim dalında uzman olmalarının sebebi, birçok dalda çeviri yapıp uzmanlaşmalarından kaynaklanmaktadır.
İslam dünyası matematiğe o kadar çok katkılarda bulunmuştur ki bunlar hakkında konuştuğumuzda eskiden ne kadar çağdaş bir medeniyet olduğumuzu anlayacaksınız. Temel matematikten, pür matematiğin derinliklerine kadar tüm matematiksel çalışmaları görebileceksiniz. Bu dönemde aklımıza gelen ilk kişi El Harezmi’dir. Harezmi matematiğin ve cebirin babasıdır. 780 yılında Harzem bölgesinde doğmuştur. Horasan bölgesinde temel eğitimini alan Harezmi, gençliğinin ilk yıllarında Bağdat’ın bilim ve ilmin merkezi olduğunu öğrenir. O kadar bilim ve ilmi seviyordu ki yer ve mekan onun için hiç önemli değildi. Hemen Bağdat’a taşınır. Harezmi Bağdat’a geldikten sonra devrin halifesi Mem’un Harezmi’nin ilim kabiliyetinden haberdar olur. Harezmi çalışkanlığı ile Bağdat’ta gözlere girmeyi başarınca Bağdat’ın saray kütüphanesinde görevlendirilir. Burada görevlerini başarılı bir şekilde tamamlayan Harezmi yabancı eserlerin çevirisini yapmak için “Beyt’ül Hikme” de görevlendirilir. Maddi ve manevi anlamda rahatlığa kavuşan Harezmi hayatın tüm kargaşalarından uzak bir şekilde matematik ve astronomi ile ilgili araştırmalar yapmıştır.
Öyle ki Harezmi Bağdat’ta o kadar meşhur olmuş ve insanlar tarafından önemli biri haline gelmiştir ki Bağdat’tan Afganistan üzerinden Hindistan’a giden bir bilim heyetinin de başkanlığını etmiştir. Şam yakınlarında bulunan ve önemli gözlem ve araştırma merkezi olarak bölgede araştırma faaliyetleri yürüten Kasiyun Rasathanesindeki ekibin başkanlığını yapan Harezmi meridyen yaylarının (1 derecelik) uzunluğunu ölçüp yer kürenin şeklini anlama çabasındaydılar. Sincar ovasında günlerce yaptıkları ölçüm ile bugün ki yer kürenin tasvirini birebir olarak buldular.
Matematikte hiçliğin rakamı olan “0” ve matematikte bilinmeyen olarak kullanılan matematiksel sıfat olan “X” ifadesini Harezmiye borçluyuz. O kadar önemli iki matematik terimini bulan bu dahi matematikçiyi Türkiye’de maalesef yakından tanıyan kişilerin sayısı bir düzine kadardır. Öyle ki üniversitelerin eğitim fakülteleri matematik öğretmenliği bölümleride ve fen edebiyat fakültesi matematik bölümlerinde “Matematik Tarihi ve Felsefesi” adındaki derste sırf bir dönem Harezmi işlenmelidir. Maalesef… Harezmi yurda geri döndüğünde bazı çeviri kitaplarında bulunan ufak cebir problemlerini çözüme kavuşturmuş cebire dair kafasında biriken tüm bilgileri ve yeni bulguları “El-Kitab’ul Muhtasar fi’l Hesab’il cebri ve ‘l Mukabele” adlı kitapta toplamıştır. Bu kitapta 0 sayısının varlığından bahsetmiş üstelik bilgisayar bilimlerinin temeli olan 2’li sayı sisteminin de kurallarını tanımlamıştır. Kitabın girişindeki şu önsöz ise bizlerin içine mutluluk düşürmektedir.
“Algoritma şöyle diyor: Rabbimiz ve koruyucumuz olan Allah’a hamd ve senalar olsun.”
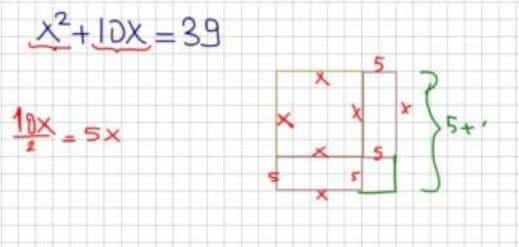
Bugün matematiğin bir alt dalı olan “cebir” dalını ilk ağzına alan Harezmi’dir. “El- cebr” ifadesi olarak kitabında geçen bu sözcük daha sonraları Avrupalılar tarafından alınarak değiştirilmiştir. Aynı bilinmeyene verilen “X” gibi… Doğunun ve batının ilk cebir kitabı olan kitapta bugün kullanılan ikinci dereceden denklemlerin nasıl çözüme kavuşacağı anlatılıyordu. Harezmi’nin çözmeye çalıştığı soru,
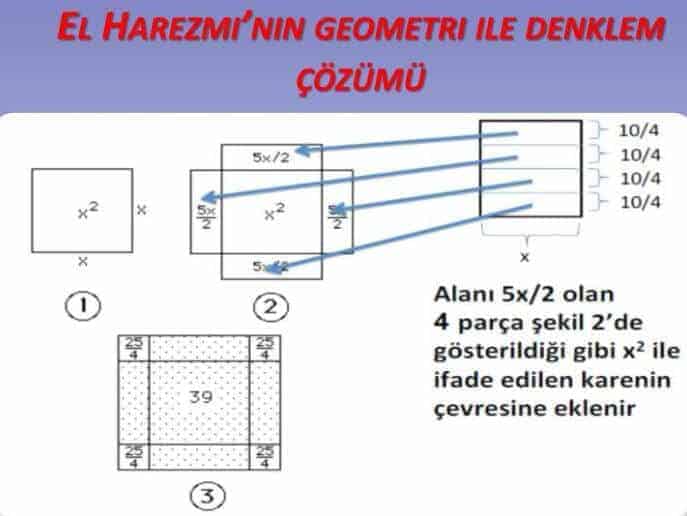
denklemiydi. Kitabı okuyan okur yaklaşık 3 saniyede cevabın 3 olduğunu anlamıştır fakat Harezmi için bu yıllarını almıştır. O dönemin matematiğini göz önüne aldığınızda bu soruyu çözmek milenyum soruyu çözmekten daha zor duruyordu. Peki Harezmi nasıl çözmüştür bu soruyu? Karelere ayırma metoduyla bir kenarı x birim olan biçimindeki kareyi ve daha sonra alanı olan etrafını saracak 4 tane dikdörtgenle çevrelenmiştir. Zaten 4 tane ifadesi 10x’e eşit olacaktı… O dönemlerde bu düşünce tarzına sahip olmak, bu şekilde düşünebilmek tabir-i caizse her baba yiğidin harcı değildi…
Karelere ayırma methodu ile ikinci dereceden bir denklemin sonucunu bulan El – Harezmi bu çözüm yöntemi ile matematik dünyasının çok önemli yol katetmesine olanak sağladı. Onun çözümünden önce ne yazık ki bu şekilde dereceye sahip denklemler çözüme kavuşturulamıyordu.
El – Harezmi’nin matematiğe katkısı sadece bununla da kalmamıştır. Sayı sistemlerine verilen rakamların düzenlemesini tekrar yapmış, “Hiç” olarak kabul edilen “0” rakamını da literatüre kazandırmıştır. Peki neden “0”? Bunun hakkında kesin bilgilere ihtiyacımız bulunmaktadır. Genel olarak rakamlar üzerinde bulunan açılara göre nitelendirilmiştir. Mesela “1” sayısına baktığımızda içinde sadece 1 açının bulunması, “2” sayısına baktığımızda sadece 2 tane açısının bulunması gibi… Harezmi herhangi bir açıya sahip olmayan yani hiç açısı bulunmayan yuvarlak sayıyı ki buna 0 diyoruz herhangi bir açıya sahip olmadığından “hiç” şeklinde ifade etmiştir. Bu ise matematik dünyasının en önemli olaylarından bir tanesidir.
Harezmi bugün adıyla bilinen “Algoritma” ifadesini ilk kullanan ve üzerine çalışmalar yapmış ilk kişidir. Avrupalıların “Algorithmus” olarak değiştirdiği hesap sistemi olan Algoritma Harezmi tarafından o günün matematikçilerine öğretiliyordu. Ne yazık ki Avrupa bunu İslam dünyasından aldı ve kendilerine uyarlayarak tüm dünyaya lanse etmeyi başardı. Harezmi ikinci dereceden denklemlere çözüm getirmişken dönemin en önemli matematik bilginlerinden Abdül – Hamid İbni Türk o kadar esrarengiz bir çözüm getirmiştir ki 14 yy. Avrupalılar ilk defa “Quadratik Denklem” ifadesini kullanabilmişler. Bugün Harezmi’nin yaptığı bu çözüm yoluna farklı bir bakış açısı getiren İbni Türk şayet ikinci dereceden bir denklemin diskiriminantının 0’dan küçük olması halinde çözümünün mevcut olamayacağını geometri kullanarak ispat etmiştir. Avrupalı matematikçiler bu çözümden anca 13. yy’dan sonraki dönemlerde haberdar olabilmişlerdir. Her zaman açıkça söylemekte fayda var ki İslam Dünyasındaki (o dönemler) bilimsel gelişmeler her zaman ufuk açıcı düzeydeydi. Matematik ile değil tüm bilim dallarıyla…
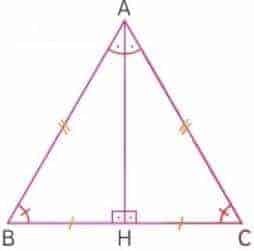
Sözde Pisagor tarafından bulunan ve onun ismiyle adlandırılan bir dik üçgendeki kenarların arasındaki ilişkiyi gösteren “Pisagor Teoremi” ile çok yakından ilgilen ve üçgenler ister dik isterse ikizkenar üçgen olması halinde yine bu teoremin uygulanabileceğini ifade eden İslam Dünyası matematikçisi Sabit İbni Kurre’nin (825 – 901) yaptığı çalışmalar matematik dünyasını olağanüstü etkilemiştir. Bugün ikizkenar dik üçgenin tepe noktasından indirilen ve tabanı iki eşit parçaya ayıran dikmenin “Pisagor Teoremi” ile gösterileceğini ifade etmiştir. (Okurun temel ikizkenar üçgen kuralını aklına getirmesini istiyoruz.)
Ömer Hayyam’ı yani diğer adıyla “Çadırcı” lakaplı dehayı geçmeden olamazdı. O kadar deli bir bilgindi ki adeta matematik adına konuşmak gerekirse ipin üzerinde cambazlık yapıyordu. Biraz matematiksel olarak konuşmak gerekirse, üçüncü dereceden eline aldığı herhangi bir denklemi (bu denklemin genel formülü olmak kaydıyla) koniklerin kesiştirmesi ile oluşan eğrinin çözümü ile bulmaktaydı. şeklinde olan denklemleri ve biçimindeki koniklerin denklemiyle elde ediyordu. Bu ise inanılmazdı. Düşünün ki henüz klasik matematik dönemi ve modern matematik dönemi ortada yokken bu şekilde bir düşünüşe sahip olmak gerçekten tüyleri diken diken etmeye yetiyordu. En ilginç olan mesele ise yıllarca çözüm bekleyen ve İngiliz matematikçi Andrew Wiles tarafından 1994’lü yıllarda çözüme kavuşturulan Fermat’ın Son Teoremi’nin çözümünün olamayacağını çoktan söylemişti. Ömer Hayyam, “Fermat’ın Son Teoremi’nin özel bir hali olan denkleminin tam sayılar üzerinde çözümünün olamayacağını göstermiştir. “Hayyam üçgeni” olarak ifade edilen ve bizlerin Binom üçgeni olarak bildiği aşağıdaki üçgeni de bulan Ömer Hayyam olmasına rağmen Pascal ve Newton’a mal edilmiştir. Matematik tarihinde bu şekilde yüzlerce örnek verebiliriz.