Hepimiz günlük hayatta çarpma, bölme, toplama, çıkarma gibi basit konuları aklımızdan yaparken zorluk çekiyoruz. Bunun için sizlere matematiği kolaylaştıran yöntemleri göstereceğiz. Bunları aklımızdan hesaplarken hem zamandan kazanacağız hem işlem yükünden kurtulacağız.
Sonu 5 ile Biten Bir Sayının Karesini Almak
Sonu 5 olan biten sayıların karelerini alırken sizde farketmişseniz her zaman 25 ile bitiyor. Öyleyse, kısa yoldan 25 ‘in önündeki sayıları nasıl oluşturabiliriz.
Çarpmak istediğiniz sonu ve 5 ‘le biten bir sayının solundaki sayıya – 1 – ekleyin ve eklenmeden önceki sayıyla çarpın.Sonra da yanına 25 ekleyin. Örneğin;
25 x 25 = ? bu sayının solundaki rakam 2 ve buna 1 ekliyoruz (2+1) x 2 = 6 buluyoruz. yani 25 in solundaki rakamımız 6 ve böylelikle sonucumuz 625 tir. Başka örnek alırsak elimize 35 x 35 = ? Son iki rakamımız 25 her zaman bunun solundaki rakam ise (3+1) x 3 = 12 ve sonucumuz ise 1225 tir.
3 basamaklı sayıda bunu uygularsak Örnek: 105 x 105 = ?
Sonucumuz yine 25 ve solundaki rakamı bulmak için (10+1) x 10 = 110. Böylelikle cevabımız 110 25 ‘tir.

15 ile Çarpma
Her hangi bir sayıyı 15 ile çarparken, çarptığımız sayının yanına 0 koyup kendisinin yarısıyla topluyoruz. Örneğin; 42×15 için 42’nin yanına 0 koyup 420 yaptıktan sonra yarısı olan 210 ile toplayıp 630’u buluyoruz.
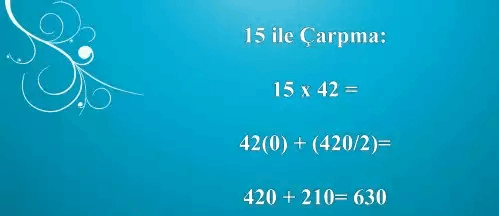
Hızlı Bir Şekilde Bir Sayının Küp Kökünü Almak
1 2 3 4 5 6 7 8 9 10
1 8 27 64 125 216 343 512 729 1000
İlk önce küp kökünü alacağımız sayıyı belirleyelim. Mesela 314432 sayısını alalım;
İlk olarak yapmanız gereken son 3 basamak ile ilk üç basamağı birbirinden ayırmak. İlk üç basamağımız 314 ve yukarıda bakıyoruz 314 hangi aralıkta diye.( 6 nın küpü = 216 ile 7 nin küpü = 343 arasında ama 7 nin küpünden küçük olduğu için 6 nın küpünü alıyoruz). Aralıktan sayımızı belirliyoruz ilk sayımız 6
İkinci olarak son rakama bakıyoruz ve son rakamımızın küpünü alarak diğer sayımızı buluyoruz. Son rakamımız 2 ve 23 = 8. Buna göre diğer sayımız 8 olacak, böylelikle 683 = 314432
Daha iyi anlamamız için başka sayı belirleyelim. Mesela 12167;
İlk olarak yapmanız gereken son 3 basamak ile ilk iki basamağı birbirinden ayırmak. İlk iki basamağımız 12 ve yukarıda bakıyoruz 12 hangi aralıkta diye.( 2 nin küpü = 8 ile 3 ün küpü = 27 arasında ama 3 ün küpünden küçük olduğu için 2 nin küpünü alıyoruz). Aralıktan sayımızı belirliyoruz ilk sayımız 2.
İkinci olarak son rakamın küpünü alıyoruz ve oda bizim ikinci sayımız oluyor. Sonra rakamımız 7 ve onun küpü ise = 343 ikinci sayımız ise 3 tür. Buna göre 23 ün küpü = 12167.

İki Basamaklı ve Daha Büyük Sayıların 11 ile Çarpımı
Çarpmanın sonucunu bulmak için,çarpılan sayının rakamlarını sabit tutarak bu rakamlar arasına rakamların sayı değerlerinin toplamını koyuyoruz. Mesela 24 x 11 olduğu gibi
24 ün ortasına rakamların toplamını koyuyoruz ve sonumuz 264. Eğerki rakamlarımız toplamı 10 dan büyükse mesela 78 x 11 = ilk rakamımızı 1 artırıp ortadaki sayıların toplamının son rakamını ortaya yazıyoruz. 7 + 8 = 15; 5 rakamını ortaya yazıyoruz ve soldaki 7 rakamımızı bir artırıyoruz sonucumuz 858 oluyor.
Eğer ki daha büyük sayılar ile çarpıyorsak. mesela 775 x 11 = ?
İşlemi sağdan sola doğru toplayarak yapacağız. Sondaki rakamımız her zaman aynı yani 5 tir. Daha sonra (5+7) = 12 rakamımız 10 dan büyük o yüzden sondan birinci rakamımız 2. daha sonra sağdan sola toplayalım (7 + 7) = 14 daha önceki rakamımız 10 dan büyük olduğu için 14 ün üzerine 1 ekliyoruz ve 15 ediyor. Yani sondan 3. rakamımız 5 tir. Bu rakamımız da 10 dan büyük olduğu için son rakama 1 ekliyoruz ve sonucu buluyoruz. Son rakamımız 7+1 = 8 tir ve cevabımız. 8525 tir.
Başka örnek çözelim. 1234 x 11 = ?
son rakamımız 4 tür. Daha sonra sağdan sola toplayarak gideceğiz. 4 + 3 = 7 sondan birinci rakamımız 7 dir. Devam edelim 3 + 2 = 5 sondan ikinci rakamımız 5 tir. 2 + 1 = 3 ve sondan üçüncü rakamımız 3 tür. Son rakamımız ise 1 dir aynen yazıyoruz. sonucumu 13574 tür. Unutmayalım eğer rakamlar toplamı 10 dan büyük olsaydı 1 ekliyorduk son rakamı yazıp.
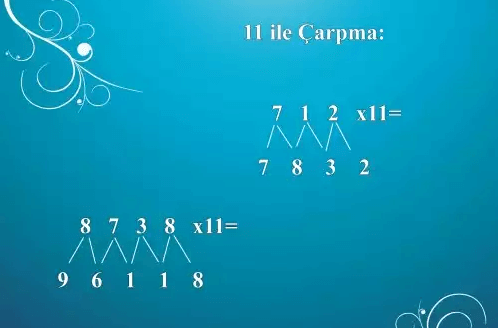
Şimdi şekle bakarak aşağıdaki örnekleri inceleyelim.
712 x 11 = 7832
Başka örnek 8738 x 11 = 96118
Herhangi Bir Sayının % ini Kısa Yoldan Almak
Mesela 42 sayısının %15, %95, %60 nı bulalım. İlk önce 42 nini %100 nu buluyoruz. 42 %50 sini 21, daha sonra 42 nin %10 ini buluyoruz, yani 10 bölümü demek buda 4,20. Bide 42 nin %5 ini buluyoruz buda 4,2 nin yarısı yani 2,10 dur.
42 nin %15 ni alırsak %10 + %5 tir buda 4,20 + 2,10 = 6,30 dur.
42 nin %95 ni alırsak %100 – %5 tir buda 42 – 2,10 = 39,90 dır.
42 nin %60 ni alırsak %50 + %10 dur buda 21 + 4,20 = 25,20 dir.
Eğer uzun yoldan 42 nin %15 ni alacak olsaydık, 42 x 15 / 100 = 6,30 olacaktı.

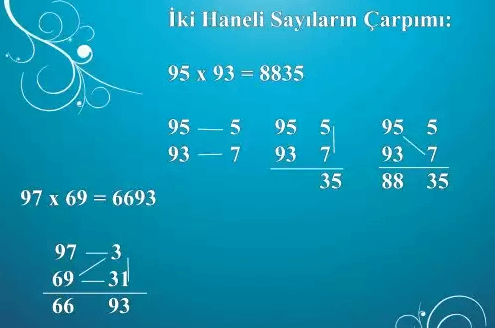
İki Basamaklı Sayılar Arasında Çarpım ( Özellikle 100’e yakın sayılar için)
İki basamaklı sayılar arasında çarpım yaparken, önce iki sayıyı da 100’den çıkarıp sonucu yanlarına yazıyoruz. Bu sonuçları çarptıktan sonra çıkan sonucu yazıyoruz. Son olarak, 100’den çıkararak bulduğumuz sayılardan birini, hemen çaprazındaki sayıdan çıkararak az önceki sonucumuzun soluna yazıyoruz. Resmi inceledikten sonra kalem bile kullanmadan yapabileceğiniz basit bir yöntem.
3 Basamaklı Sayıların Çarpımı
3 basamaklı sayıları çarparken, 100’den çıkarıp yanlarına sonucu yazıyoruz. Bu sonuçları birbiri ile çarpıp en sağa çıkan sonucu yazıyoruz ve 100’den çıkararak elde ettiğimiz sonuçlardan biri ile üç haneli sayımızın birini toplayıp sağa yazıyoruz ve tam sonucumuz ortaya çıkıyor. Şekildeki örneği inceleyerek daha iyi anlayabilirsiniz.

3 Basamaklı Bir Sayı ile 1 Basamaklı Bir Sayının Çarpımı
Aslında 3 basamaklı sayı ile 1 basamaklı sayıyı aklımızdan çarpmak biraz zamanımızı alsa da, sizlere bunun daha basit ver pratik yolunu göstereceğiz.
- İki tane sayı seçelim. 320 x 7 = ?
- İlk olarak 3 basamaklı sayımızı basamaklarına ayır gibi iki parçaya ayırıyoruz: 320 (320 + 20)
- İkinci olarak 300 çarpı 7 ve 20 çarpı 7 yapıyoruz.
- Son olarak 300 x 7 = 2100 ve 20 x 7 = 140 bu bulduğumuz değerleri toplayarak sonucu buluyoruz. Kendiniz bu sayıların daha karmaşığını rahatlıkla artık aklınızdan yapabilirsiniz.
2100 + 140 = 2240

Sihirli Sayı 1089
Şimdi rakamları farklı 3 basamaklı bir sayı tutalım aklımızdan(Örneğin; 684). Bu tuttuğumuz sayı tersten yazalım (684 sayısını tersten yazarsak 486). Şimdi büyük olan sayıdan, küçük olanı çıkaralım. (684 – 486 = 198) Şimdi çıkan sonucumuzu bu sayının tersi ile toplayalım (198 + 891 = 1089), topladığımız zaman sizinde gördüğünüz gibi sonucumuz 1089 çıkacak. Siz de farklı sayılar deneyerek aynı sonucu bulabilirsiniz.


