Merhaba arkadaşlar ele alacağım bu konu mühendis beyinler sitesindeki ilk yazım olacak. Sizlere matematik alanında yazılar hazırlamayı düşünüyorum. Matematik ve Sonsuzluk Kavramı çok karıştırılan bir konudur. Yazımda elimden geldiğince bunu size açıklamaya çalışacağım. Öncelikle elimize bir ışın parçası alalım. Başlangıç noktasına 0 (sıfır), bitiş noktasına ise 1 (bir) diyelim.
Sonsuzluk Kavramı Nedir
Şimdi 0 ile 1 arasındaki yazılabilecek sayı adedini düşünelim. Evet, şu an düşünüyorsunuz ve, evet sanırım bir yanıtınız var: sonsuz mu? İnsan beyni cevabına ulaşamadığı çoğu şeyi bir kalıba oturtur ve bundan dolayıda sonsuz yanıtını verir. Bu yanıt doğru da geçerli bir yanıt fakat gerçekte değildir. Küçük bir örnek ile problemi şekillendirelim.
Yazımızın başında bir ışın parçası almıştık. Şimdi elimize bir cetvel alalım. Ve kendimize göre bir başlangıç belirleyerek oraya 0 (sıfır) diyelim. Bitişe de 1 diyelim. Şimdi bir daha düşünelim: 0 ile 1 arasındaki sayı adedi sizce nedir?
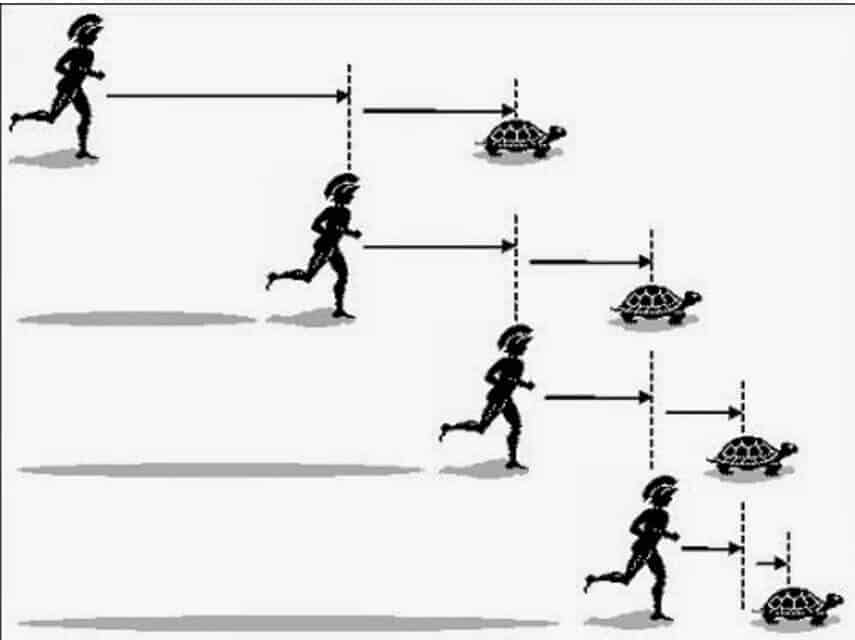
Şimdi sonsuz diyemiyoruz değil mi? Aslında da 0 ie 1 arasında sonsuzluk mevcut değildir. Parçalayamayacağımız değerler vardır. Epsilon sayısını (0′ a en yakın sayı) ben bu şekilde görüyorum. Epsilondan küçüğü yoktur. Eğer her birimi parçalayabilseydik Zenonun oku hiçbir zaman hedefe ulaşamazdı.
Demem o ki: 0 ile 1 arasındaki sayıların sayısına sonsuz diyemeyiz. Ne kadar olduklarını ise ancak ve ancak küçültülemeyen bir birimin varlığının değeri bulunur ise o zaman aradaki sayı bakımından bilgimiz olur. O zamana kadar da sonsuz terimi yerine belirsiz yanıtı gayet mantıklı olmakla birlikte matematikteki sonsuzluk sıfatının amacını yitirtmemiş oluruz.
Yani reel deki sonsuzluğu matematiğe indirgeyemeyiz. Ayrıca pi sayısınında sonsuz olmadığını bu şekilde de görmekteyiz. Bir cetvel alıp başlangıcına 3,14 deyip bitişinede 3,15 der isek reelde ki sonsuzluğun sanırım matematikte geçerliği olmadığını göstermiş oluruz. Eğer doğrular üzerine değil gerçekler üzerine çözümleme yaparsak , ne kadar soyut isek o kadar somut oluruz.
İlginizi çekebilir :