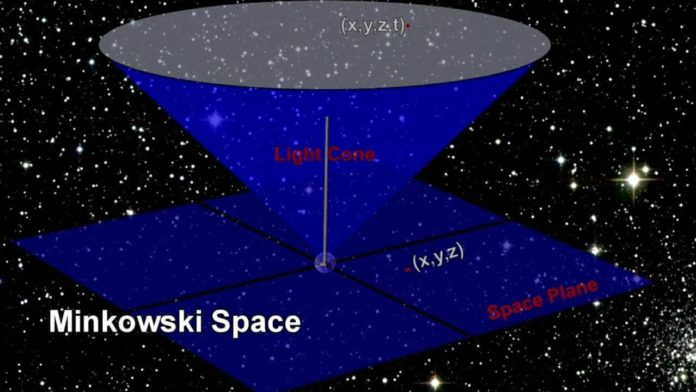
Matematiğin tanımladığı ilginç uzaylar vardır. Öklid uzayı, Riemann Uzayı gibi. Bunları biliyorsunuz. Fakat bir de derin matematikte çok ilginç ve bir o kadar da gerçek farklı bir çalışma alanı vardır. Minkowski Uzayı…

Uzay – Zaman diye diye dilimizden düşüremediğimiz fiziksel olgunun açıklanmasını sağlayan bu uzay Hermann Minkowski tarafından ortaya atılmıştır. Matematiğin tüm alanlarında olduğu gibi ilk başta çok saçma ve anlamsız gibi görünmesine karşın daha sonraları Kuramsal fizik dediğimiz alanda çığır açmıştır.
Çok teknik bir açıklamadan uzak durmakta fayda var. Hepimiz uzayın üç boyutlu olduğunu ve “Hadi bu boyutları say” şeklinde de bir soru sorulduğunda “En, boy, yükseklik” şeklinde cevap verdiğimizi biliriz. “Peki 4 boyutlu uzayı açıklar mısın?” dediklerinde de “Zamanı eklersek 4 boyutlu olur” şeklinde cevap veririz. İşte sizin bahsettiğiniz şey tam da Minkowski uzayıdır. Einsteinin boyutlar hakkında yorum yaptığı ve çalışmalarını sürdürdüğü, özel görelelik adı altında bahsettiği tüm fizik kanunları bu uzay ile ilgilidir. Peki matematik açısından nasıl tanımlanmaktadır?
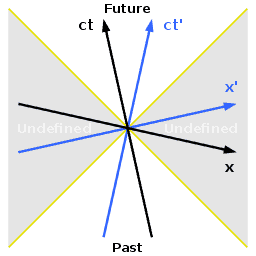
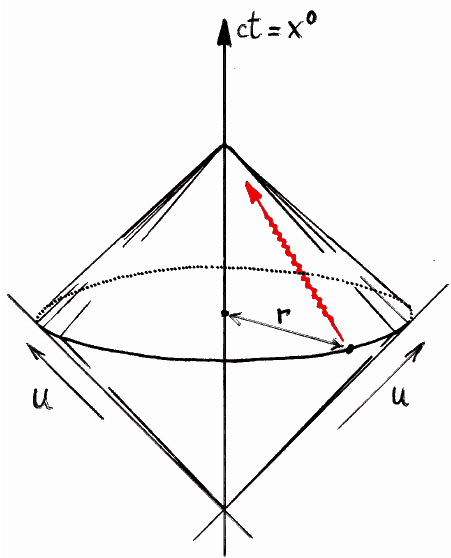
Yukarıdaki diagram “Minkowski Diagramı” olarak bilinir. Bu diagramda herhangi bir olayın gerçekleşme ya da gerçekleşmeme durumu ile gelecek ve geçmiş durumları arasında bir bağlantı kurulabileceğini göstermektedir. “Geçmiş” ile “Gelecek” arasındaki tam kesişim noktası ise olayın gerçekleştiği anı göstermektedir. Işık hızının “c.t” ile gösterildiği diagramda ışık hızının aşılamayacağı da göz önüne alınarak, ışık hızının geçildiği bölgeler tanımlanmamıştır. Bu diagram aslında bizlere “Minkowski Eğrisi”‘nin bir kesitinin göstermektedir. Hemen uzayımızın kesitini ele alalım.
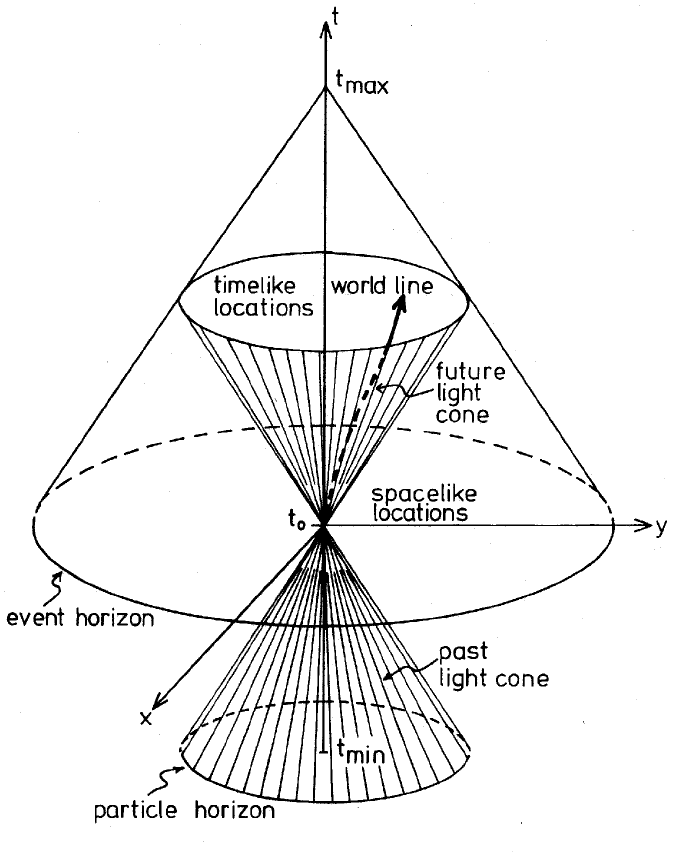
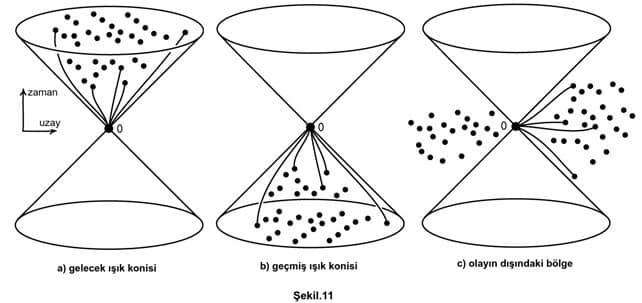
Gözümüze çarpan bu üç koni geçmiş zamanı ve şimdiki zamanı göstermektedir. Tmax olarak verilen ise, ışık hızından (yukarıdaki gibi) sonraki zamanı temsil etmektedir. Bu da Minkowski eğrisinde sıfır olarak kabul edilir. Dikkat edelim ki, “Olay çizgisi” olarak tanımlanan eğrisinin orta çapında kesişim olayın gerçekleştiği zamandır. Üç boyutlu eğride ( x,y,z axis) altta kalan koni zamanın gerilediğini zamanın minimum düzeye indiğini göstermektedir. Işık hızına ne kadar yaklaşırsak o kadar olayın gerçekleşme zaman aralığı azalmaktadır.
Yukarıdaki şeklin daha iyi anlaşılması adına daha net renkli bir eğri çizebiliriz. Bu şekilde daha net bir şekilde anlayabiliriz. Şu iki koninin orta noktası gözlemcinin yani bireyin olduğu noktadır. Herkes ordadır… Fakat geçmiş ve gelecek için tam net şeyler söylenmemektedir. Bu durumu açıklayan en önemli örnek ise sizlerin belki de çok iyi bildiği “ikizler paradoksudur.” Konu ile ilgili yazımızı bulabilirsiniz.
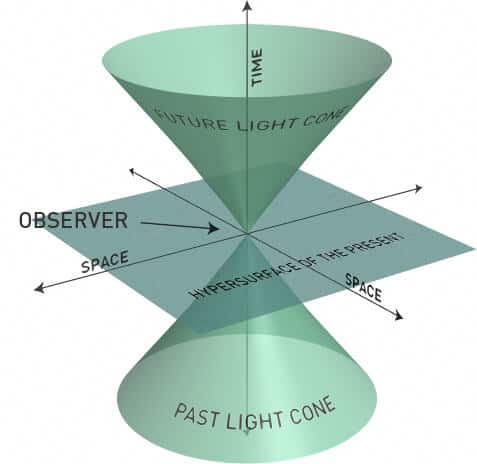
Matematikte ise Minkowski uzayı farklı bir tensör bağlamında ortaya atılmış bir uzaydır. Belirli kuralları olan bu kurallar dahilinde farklı geometrik şekilleri bulunan bir uzaydır. Öklid geometrisini düşünün, bu geometrinin bir elemanı olan üçgenleri de… Hemen buna pat diye örnek verirsek Bond’i koordinat sistemi bu uzayın bir elemanıdır.
Bu ise kesilmiş halde, düzleme aktarılmış olarak bizlere,
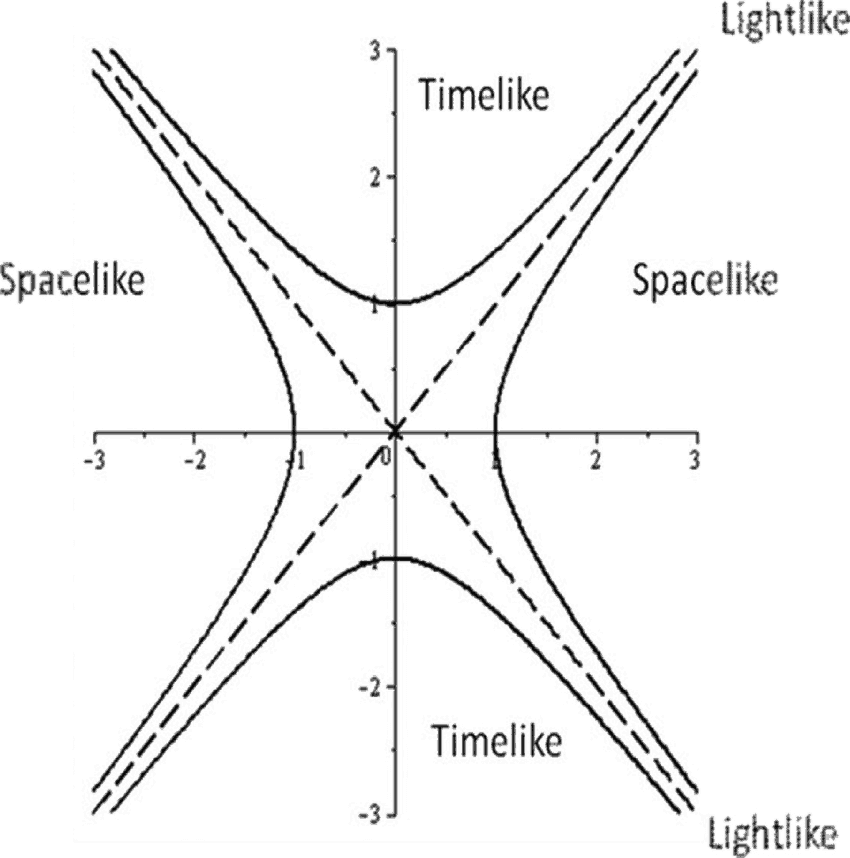
şu şekilde bir görüntü elde etmemizi sağlar. Bunun nasıl yorumlanacağını artık biliyoruz. Timelike ve Spacelike olarak ikiye ayrılan bu “Minkowski Uzayının” 0 noktasının gözlemcininin yeri olduğunu spacelike olarak gösterilen alanının bu ışık hızından dolayı tanımlanmadığı daha düzgün şekilde yok sayıldığını göreceğiz. Diğer Timelike bölgesi ise geçmiş gelecek ve şuan olarak üç kısımda daha derin olarak incelenir.
Matematikte temeli ise Poincare grubu ile ilişkilidir. Poincare disk methoduna göre belirli bir zaman hesabında Öklid uzayının bakışım grubu ile tam zamanlı eklemelidir. Bu tanımdan bişey anlamadık. Öklid uzayı sadece uzaysal eksenlere sahip iken Minkowski uzayı “ct” zaman skalesine sahiptir. Bunu da yukarıda bahsettik. Poincare grubunun formülü okur tarafından merak ediliyorsa korkmasın hemen aşağıda ilk olarak Poincare disk method formülü daha sonra Minkowski diagram denklemini görebilirsiniz. Dikkat “ct”‘yi ihmal ediniz.
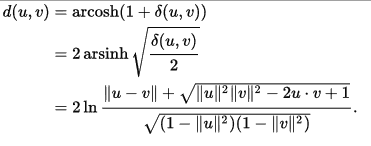
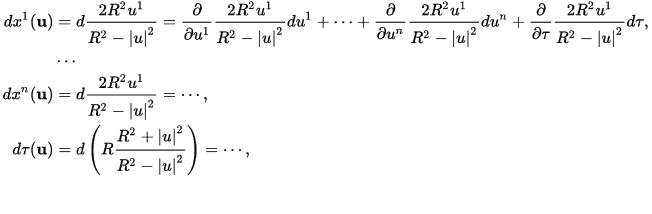
ifade edilir. Birinci türevinde varyasyon hesabı yapmamıza gerek yoktur. Umarım biraz olsun anlamışızdır. Zor bir bilim matematik… Son olarak yazıyı Hermann Minkowski’nin çok güzel bir sözü ile bitirelim…
oh,o einstein derslerini sürekli geçiştiriyor. onun böyle bişey yapacağını hiç düşünmemiştim.