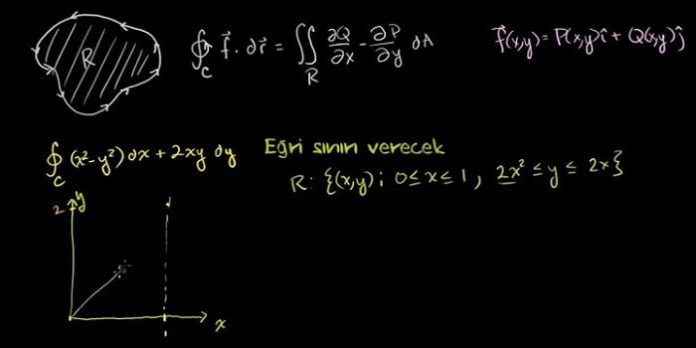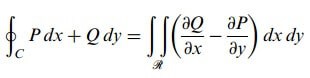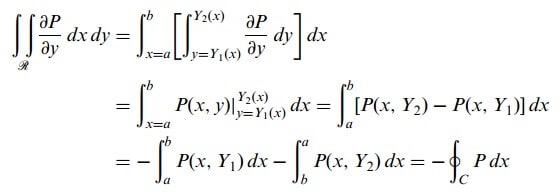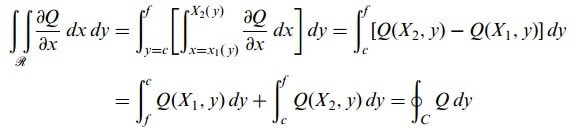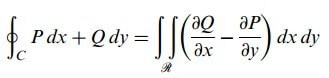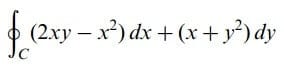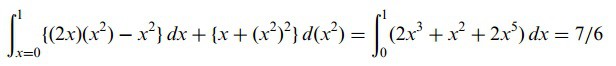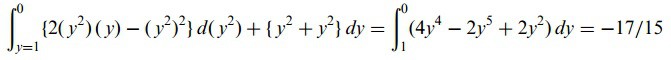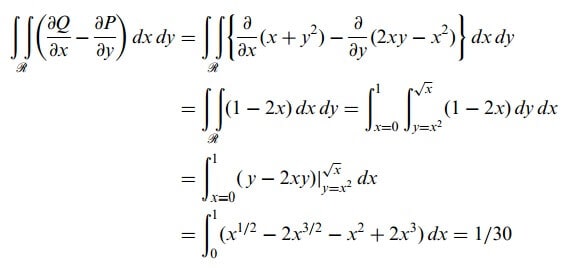Düzlemde Green Teoremi

Merhaba arkadaşlar bu yazımızda sizlere düzlemde green teoremi ve bunun yanı sıra konuyu daha iyi kavramamız için düzlemde green teoremi ile ilgili örnekler çözeceğiz. P, Q, ∂P/∂y, ∂Q/∂x  basit kapalı bir C eğrisiyle sınırlanan basit bağlantılı R bölgesinde tek değerli ve sürekli olsun. Bu taktirde;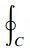 ifadesi C nin kapalı ve pozitif yönlü olduğunu göstermek üzere

sağlanır.

Bu teorem iki veya daha çok kapalı eğri ile sınırlandırılan bölgeler (yani çok bağlantılı bölgeler) için de geçerlidir.

Düzlemde Green Teoremi Örnekler

1.Örnek) C koordinat eksenlerine paralel herhangi bir doğru tarafından en çok iki noktada kesilen bir kapalı eğri ise Düzlemde Green Teoremi ‘ni ispat ediniz.

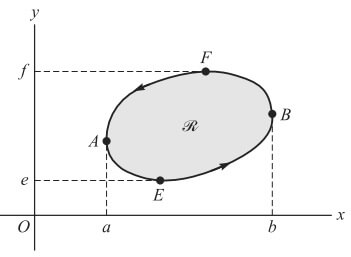
AEB ve AFB eğrilerinin denklemleri sırasıyla y = Y₁(x) ve y = Y₂(x) olsun (Şekil 1 ‘e bakınız). Eğer R bölgesi C ile sınırlı ise,

bulunur. O zaman

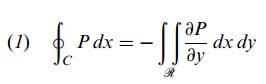
olur.

Benzer olarak EAF ve EBF eğrilerinin denklemleri sırasıyla x = X₁(y) ve x = X₂(y) olsun. Bu taktirde

dir. O zaman

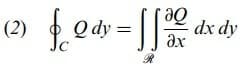
dir. Eşitlik (1) ve (2) yi toplayarak

istenen sonucu buluruz.

2.Örnek) C eğrisi y = x² ve y² = x ile sınırlanan bölgenin kapalı bir eğrisi olmak üzere

için Düzlemde Green Teoremi ‘ni gerçekleştiriniz.

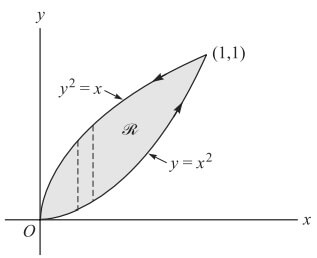
y = x² ve y² = x düzlem eğrileri (0,0) ve (1,1)’ de kesişir. C eğrisinin çizilmesindeki pozitif yön şekil 2 ‘de gösterildiği gibidir.

y = x² boyunca, eğrisel integral

‘ya eşittir.

y² = x boyunca eğrisel integral

‘ya eşittir. Bu durumda istenen eğrisel integral = 7/6 + (-17/15) = 1/30 dur.

dur. Böylece Düzlemde Green Teoremi sağlanmış olur. Bugün sizlere düzlemde green teoremi ve düzlemde green teoremi ile ilgili örnekler çözdüm. Bu konumuzun devamı olan yüzey integralleri konusunda görüşmek üzere.