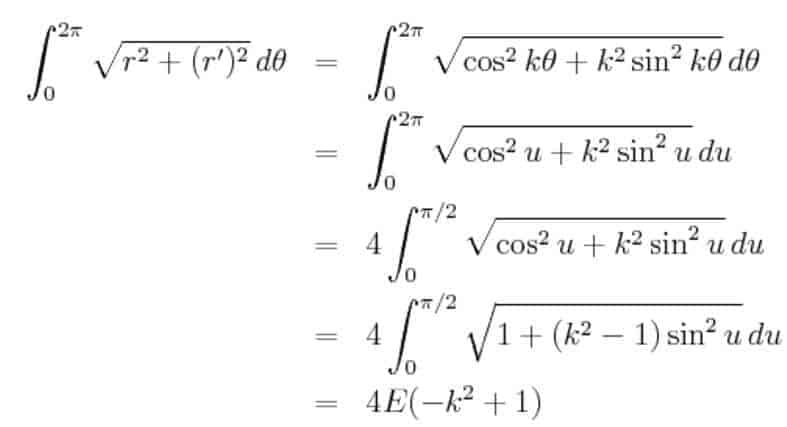Matematikte ilginç nesnelerin olduğuna şahit olmaktayız. Topolojiden, geometriye, analizden, diferansiyel topoloji/geometriye kadar birçok alanda insanı hayrete düşüren nesneler bulunmakta. Analitik Geometri ve ileri seviye uğraş alanlarında gül biçimi olarak bilinen fonksiyon grafikleri matematikçilerin gül bahçesini süslemektedir.
Matematiksel olarak belirli bir başlangıç noktası ve bitiş noktasına sahip eliptik integrallerle hesaplanan ve açısının cinsine göre değişen bu güller bugün süsleme sanatında önemli yere sahiptir. Özellikle mimarı alanda yapılan desenler aşağıda vereceğimiz integral yardımıyla hesaplanabilmektedir.
biçimi ile ifade edilmektedir. İntegralin hesaplanabilmesi için herhangi bir kapalı form maalesef bulunmamaktadır. Bunun yerine, sonucun tanımlandığı özel bir fonksiyon olan E (x), “ikinci tür tam eliptik integral” ile tanımlanır. Bu ise biraz daha karışık ve insanı çıldırtan düzeyde olabilir. Yukarıdaki integrali hepiniz hesaplayabilir ve yorumlar üretebilirsiniz. Şimdi ise E(m)
integralini tanımlayalım.
Gülün uzunluğunu bu formül ile kıyas edelim;
olacaktır. Gülün yay uzunluğu,
r=cos(kθ)
biçiminde olacaktır ve burada gösterilen açı değeri 0’dan 360 dereceye kadar tarama yapacaktır.
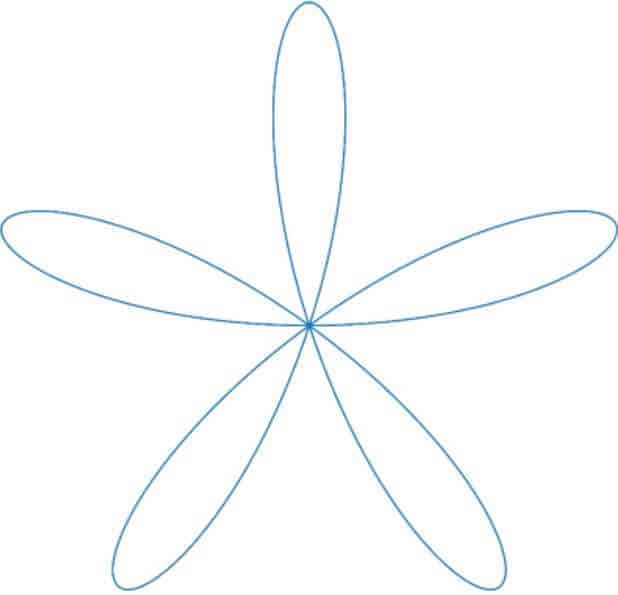
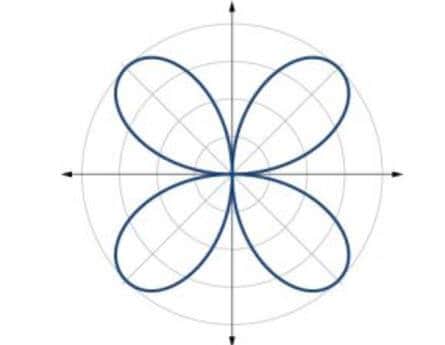
Şimdi yukarıdaki denklemle hesaplama yaptığımızda bu sonucunun 20.01 olduğunu hesapladık. 4 E(-24) = 21.01. (Yukarıda görülen gül) Fakat integral ile hesaplama yaptığımız da verilen değerin aynı olmadığını fark ettik peki neden? Yani integralle olan hesaplama ile sonda E’li formülle hesaplanan değerde bir farklılık oluştu.
k büyüdükçe, yapraklar düz çizgiler haline gelir. Bu nedenle, k genişledikçe 4E’nin (-k² + 1) 4k’ye yaklaşmasını beklemeliyiz. Aşağıdaki E (-k² + 1) – k komutu, bu varsayım için farkın 0’a yaklaştığını göstermek suretiyle ampirik bir destek sağlar ve yakınsama oranı hakkında bir fikir verir. E (-k²) ‘nin asimptotik olarak k’ye yaklaştığını kanıtlamak mümkündür fakat bunun ispatını vermiyoruz. Şekile bakarak yorum yapabiliriz.
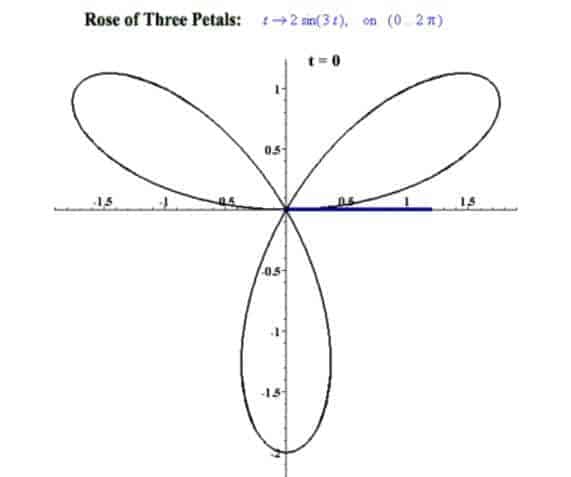
Ayrı bu güllerin bir de farklı denklemlerle karmakarışık halleri mevcuttur. 1723 – 1728 yılları arasında italyan matematikçi Guido Grandi tarafından tanımlanan “Rhodonea” isimiyle de tanımlanan gül çeşitleri aşağıdaki biçimdedir. Bu çiçeklerin polar koordinatları,
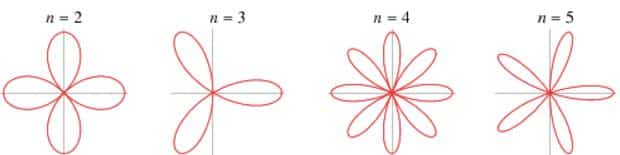
r=a.sin(nθ) ve r=a.cos(nθ) biçiminde tanımlanır. Burada “n” değerinin değişmesi ile,
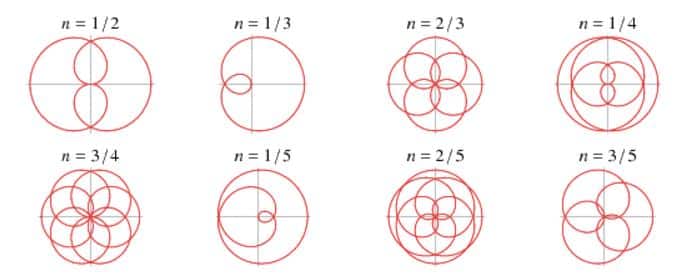
şeklinde güller oluşacaktır. Peki kutupsal gösterimi daha farklı olan güllerin biçimleri nasıl dersiniz?
n=r/s biçiminde tanımlanan gül çeşitleri ise,
Bu noktada r ile s arasındaki ilişki ile şekillerin oluşum biçimleri arasındaki bağlantıyı sizlere bırakıyorum. ( İpucu: Tek – Çift Durumu ) Bir de merak ettiğimiz irrasyonel sayılar işin içine girse yani kesir olacak şekilde tanımlamayan garip sayılarla oluşan güllerimiz nasıl olur?
Bakın bu noktada n sayısı ile ifade edilen tüm sayılar birer irrasyonel sayıdır. Adeta görsel fantaziden başka bir şey değil…
Yazı ve İleri Okumalar İçin
- johndcook.com/blog/category/math/
- mathworld.wolfram.com/Rose.html