Matematikteki milenyum sorular kategorisinde Rus Matematikçi Grigori Perelman tarafından 2010 yıllarının başında kanıtlanmış bu teorem, matematik dünyasının bir dönüm noktası diyebileceğimiz sonuçları bizlere gösterdi. Peki bizlere ne anlatmak istiyor bu çözülen ünlü problem ya da neler anlamamız gerekiyor.
Bilindiği üzere 1904 – 1905 yılları arasında Fransız matematikçi ve filozof Henri Poincare tarafından ortaya atılmış ve çözümü yüzlerce yıl sonra çözülebilmiş bir problemdir. Evet, genel olarak her yerde bulabileceğiniz şöyle bir tanım vardır: Tıkız, kenarı olmayan, basit bağlantılı yani herhangi bir deliği olmayan üç boyutlu bir çok katlının (üç boyut ve varsa daha fazlası) sadece küre olabileceğini anlatmaktadır.
Bu tanım verilirken tıkız kelimesi topoloji dersi almamış kişiler tarafından anlaşılmaz. Tıkız, iki topolojik uzay arasında sürekli gönderimlerin olduğu küme üzerine konulan isimdir. Yani daha profesyonel bir açıklama yapmak gerekirse,
X ve Y birer topolojik uzay olsun. X’ten Y’ye gönderimlerin sürekli kümesi ise C(X,Y) ile gösterilsin. Bu küme üzerine tıkız-açık topoloji kuracağız. X’te tıkız bir K kümesi ve Y’de açık bir V kümesi olsun. C (X, Y) kümesinin F (K, U) altkümesi şöyle tanımlansın: X’ten Y’ye giden sürekli bir f gönderimi, K’yi V’nin içine götürüyorsa f gönderimi F (K, U) kümesinin içindedir. Olası tüm tıkız K ve açık U için F (K, U) altkümelerinin topluluğu, C (X, Y) kümesinde tıkız-açık topolojinin bir alt tabanını oluşturur. Eğer X kümesi yalnızca bir noktadan oluşmuşsa, C (X, Y) kümesi tıkız-açık topolojisiyle Y topolojik uzayına homeomorfiktir
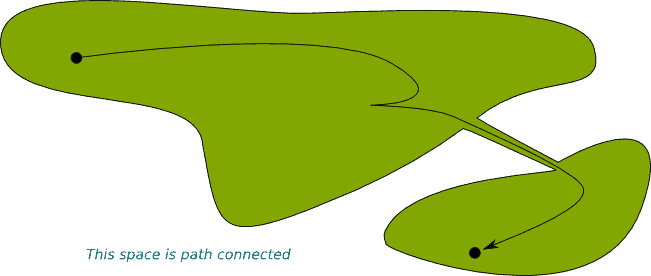
Güzel… Hemen hemen kafamızda birşeyler canlandı. Ya basit bağlantılı ya da eski matematiksel söylemiyle çoklu bağlantılı olmayan… Hemen topoloji olarak tanımını verelim. Topolojide, geometrik bir nesne veya uzaya yol bağlantılıysa ve iki nokta arasındaki her yol sürekli bir şekilde bir diğerine dönüştürülebiliyorsa basit bağlantılı (veya 1-bağlantılı) adı verilir. Aklımıza gelmesi gereken en önemli basit bağlantılı şekil bir küredir. Yani küre üzerinden alınan herhangi bir döngü tek bir noktaya büzülebilir. Mesela elinize bir top alın ve bu topun etrafına bir lastik bağlayın, ellerinizi kullanarak çaptan başlayarak uç noktaya kaydırdığınızda kutup bölgesinde bunu tek bir nokta haline getirebilirsiniz. Yani,

aynen bu şekildedir. Çok katlılık ise topoloji de bir soyut uzaydır. Bu uzayın çevresi tıpkı Öklid uzayına benzemektedir. Hemen yukarıdaki küreye bakabiliriz. Çevresi bir Öklid uzayı gibi değil mi? Bununla birlikte, bir çok katlı bir Öklid uzayı olmak zorunda değildir. Genel yapısı, bu basit yerel yapısından çok daha karmaşık olabilir. Çok katlının boyutu, yerel olarak benzediği Öklid uzayının boyutu olarak tanımlanır. Herhangi bir topolojik uzay içinse boyut kavramından söz etmek genelde olası değildir.
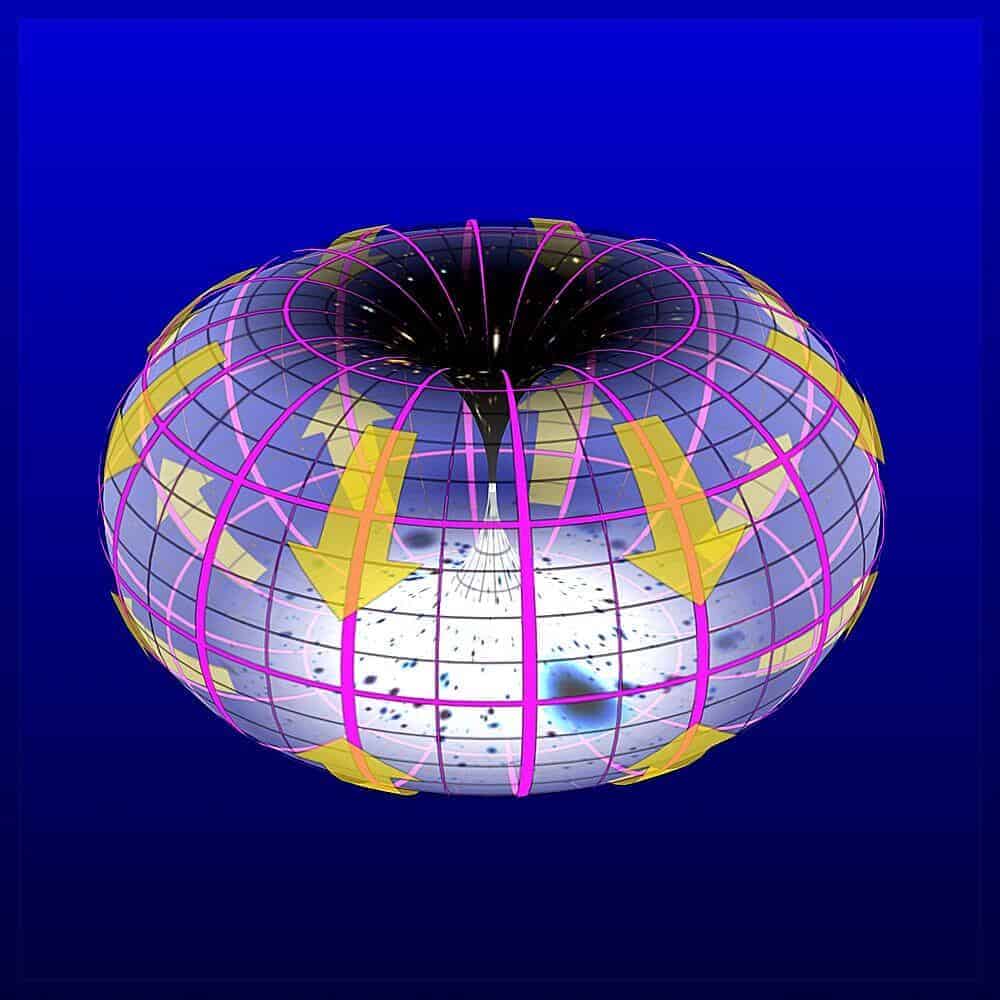
Bu çözüm ile birlikte herhangi bir döngünün bir noktada büzülebilmesi için bu topolojik nesnenin küre olması gerektiği kanıtlanmış oldu. Peki bu kadar ses getiren ünlü bir problem ne fayda sağlayacak bizlere? Aslında çığır açan çözüm bizlere evrenin topolojik yapısını görmemize katkı sağladı. Bu soru çözülmeden önce evren hakkındaki bilgilerimiz çelişkiler taşıyordu ve evrenin sonunun olmayacağı kesin olarak bilinmesine rağmen bunu gösteren bir bulgunun olmamasından dolayı matematikçiler ve fizikçilerin kafasında hep bir soru işareti vardı.
Bu bağlamda evrenin bir küre modeline değil de torus olarak nitelendirilen bir simite yakın olabileceği gözler önüne serildi. Kara deliklerin bir alt uzay olarak alınması akabinde, döngülere sahip bu uzaysal yapılar tek bir noktada maddeleri büzebilmektedir. Bu ise Poincare sanısına bir gönderme yapmaktadır.