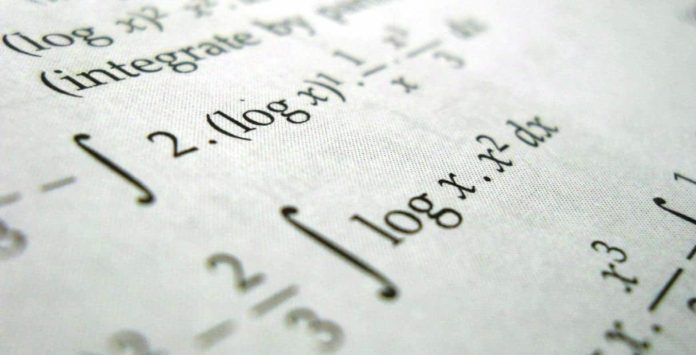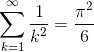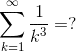Matematiğin sınırları; taylor serisi ve garip açılımları. Artık ikinci, üçüncü ya da daha fazla dereceden denklemlerle uğraşmaktan sıkıldınız mı? Aslında bakarsanız sıkılmayan bir kişi dahi bulamazsanız. Ama size çok kısa ve güzel bir yoldan bahsedeceğiz. Bu biraz daha profesyonel matematikçilerin başvurduğu dışarıdan bakınca biraz garip lakin incelendiğinde heyecan verici bir çözüm metodu…
Kosinüs ve Sinüs fonksiyonlarının seriler biçiminde ifade ediliş biçimleri vardır. Bunları birçoğunuz biliyorsunuzdur.
biçiminde tanımlanır. Birbirlerinin türevlerini alarak eşitliği kontrol edebilirsiniz. Buradaki faktöriyel ifadesinin ne anlam ifade ettiğini biliyoruz. Bu noktada herhangi bir “x” ifadesi ile sin(x) ve cos(x) ifadelerinin değerlerini sonsuza doğru yola çıkan seriler yardımıyla hesaplayabilmekteyiz. Sadece trigonometrik fonksiyonlar değil birbirinden güzel ve hoş fonksiyonları da tanımlayabilmekteyiz. Örneğin; Exponent fonksiyon olarak bilinen 
fonksiyonunu tanımlayalım.
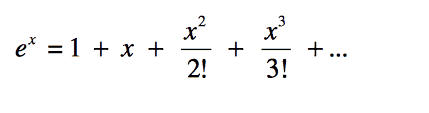
Bu açılım ile x yerine koyabileceğiniz herhangi bir sayısının e sayısının bir kuvveti olarak hesaplayabiliriz. Bakın şöyle bir örnek yapalım;
sayısını normal şartlarda nasıl hesaplarsanız? İlkokul mantığı ile 0.1 tane e=2,718.. sayısını mı çarpacağız? Bakın hemen formülde yerine koyalım. Daha sonra da hesap makinası ile hesapladığımız sonuca bakalım.
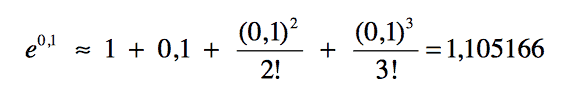
Hesap makinasında da hesap yaptığımızda,
bulmaktayız. Hemen hemen iyi yaklaşım gibi ne dersiniz? Yukarıda verilen sin(x) ve cos(x) değerli için de bir tane siz hesaplayabilirsiniz. Ama çok garip gelmedi değil mi? Merak etmeyin neyse ki elimde bir ilginç bilgi daha var. Matematik yıllar boyunca seriler ilgili birçok problemin çözümü için uğraşmıştır. Hemen hemen herkesin bildiği seriler yüzyıllar boyunca matematikçilerin ilgisini çekmiş hala da çekmeye de devam etmektedir. İlk zamanlarda serilerin doğuşu ve analizin gelişimi ile matematikçiler,
şeklindeki serileri inceleme çabasına girdi. a sayısı için şayet 0 ile 1 arasındaysa serinin değerini hesaplayabilmekteyiz. a=1 olduğunda ise serinin ıraksak yani sonsuza gittiğini biliyoruz. Peki a ifadesi 1’den büyükse ne oluyor? Bunların hepsinin cevabı yıllar içinde yapılan çalışmalar neticesinde verildi. Fakat matematikçileri zorlayan bir konu vardı? Basel problemi adı verilen problemlerin sadece bir tanesi çözülebilmiş fakat diğer değerler için henüz kimse ağzını dahi açamamıştı. Doğanın matematiği var mı? biçiminde soru sorulduğunda hemen Basel probleminin bir çözümünü verebilirsiniz.
Gördünüz mü? Ne kadar da heyecan verici bir durum. Leonhard Euler tarafından yıllarca uğraşılmış ve “Basel problemleri” ismini de bizzat kendi vermiştir. Günümüzde ise herkesin merak ettiği soru;
İçinizden biri bu sorunun cevabını verip ölümsüzlüğü yakalayabilir? Matematikte açık problem diye ifade edilen sorulardan bir tanesidir….